北師大版（2019）必修第二冊《第四章 三角恒等變換》2021年單元測試卷（2）

一、單選題

• 1．已知角α的終邊經過點（2，-1），則cos2α=（　　）

  A．- 3 5

  B． 1 5

  C． 3 5

  D． 4 5
  組卷：90引用：2難度：0.8

  解析

• 2．若sin（α+

  π

  4

  ）=5sin（α-

  π

  4

  ），則tanα=（　　）

  A． 3 4

  B． 3 2

  C． 4 3

  D． 2 3
  組卷：296引用：7難度：0.7

  解析

• 3．若tanx=-

  1

  3

  ，則sin2x=（　　）

  A． 3 5

  B． - 3 5

  C． 3 10

  D． - 3 10
  組卷：301引用：5難度：0.8

  解析

• 4．將函數y=sin2x的圖象向右平移

  π

  4

  個單位，再向上平移1個單位，所得圖象的函數解析式為（　　）

  A．y=2cos2x	B．y=2sin2x
  C．y=1+sin（2x+ π 4 ）	D．y=cos2x
  組卷：77引用：8難度：0.9

  解析

• 5．已知函數f（x）=

  3

  cos²x-sinxcosx-

  3

  2

  ，則f（x）滿足（　　）

  A．圖象關于直線x=- π 6 對稱

  B．在（ π 2 ， 3 π 4 ）上單調遞增

  C．f（ π 3 ）= 3 2

  D．當x= 11 π 12 時有最小值-1
  組卷：80引用：1難度：0.7

  解析

• 6．已知α終邊與單位圓的交點

  P

  （

  x

  ,

  3

  5

  ）

  ，且α是第二象限角，則

  1

  -

  sin

  2

  α

  +

  2

  +

  2

  cos

  2

  α

  的值等于（　　）

  A． 1 5

  B． - 1 5

  C．3

  D．-3
  組卷：173引用：4難度：0.7

  解析

• 7．已知函數

  f

  （

  x

  ）

  =

  3

  sinωx

  -

  cosωx

  （

  ω

  ＞

  0

  ）

  在

  [

  0

  ，

  π

  2

  ]

  內有且僅有1個最大值點和3個零點，則ω的取值范圍是（　　）

  A． （ 13 3 ， 16 3 ]

  B． [ 13 3 ， 16 3 ）

  C． （ 14 3 ， 17 3 ]

  D． [ 14 3 ， 17 3 ）
  組卷：92引用：1難度：0.6

  解析

三、解答題

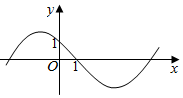• 21．已知函數f（x）=2sin（ωx+φ）（ω＞0，

  π

  2

  ＜φ＜π）的圖象如圖所示，其中f（0）=1，f（1）=0．
  （1）求f（x）的最小正周期T；
  （2）若-2＜x₀＜1，且f（x₀）=

  1

  2

  ，求

  cos

  （

  π

  6

  x

  0

  ）

  ．
  組卷：215引用：3難度：0.6

  解析

• 22．已知函數f（x）=asinx+bcosx,其中ab≠0．
  （1）若b=1，是否存在實數a使得函數f（x）為偶函數，若存在，求出a的值；若不存在，請說明理由；
  （2）若

  x

  =

  3

  4

  π

  為函數f（x）的對稱軸，求函數f（x）的單調增區間．
  組卷：178引用：2難度：0.6

  解析