2023年安徽省蚌埠市五河縣高考數學第二次質檢試卷

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．對于數集A，B，定義A+B={x|x=a+b,a∈A，b∈B}，A÷B={x|x=

  a

  b

  ，a∈A，b∈B}若集合A={1，2}，則集合（A+A）÷A中所有元素之和為（　　）

  A． 10 2

  B． 15 2

  C． 21 2

  D． 23 2
  組卷：140引用：4難度：0.9

  解析

• 2．復數

  2

  -

  i

  2

  +

  i

  =（　　）

  A． 3 5 - 4 5 i

  B． 3 5 + 4 5 i

  C． 1 - 4 5 i

  D． 1 + 3 5 i
  組卷：216引用：13難度：0.9

  解析

• 3．sin155°sin55°+cos25°cos55°=（　　）

  A． - 3 2

  B． - 1 2

  C． 1 2

  D． 3 2
  組卷：472引用：2難度：0.8

  解析

• 4．若直線y=kx+4+2k與曲線

  y

  =

  4

  -

  x

  2

  有兩個交點，則k的取值范圍是（　　）

  A．[1，+∞）

  B．[-1，- 3 4 ）

  C．（ 3 4 ，1]

  D．（-∞，-1]
  組卷：489引用：30難度：0.7

  解析

• 5．已知某地區中小學生人數如圖①所示，為了解該地區中小學生的近視情況，衛生部門根據當地中小學生人數，用分層抽樣的方法抽取了10%的學生進行調查，調查數據如圖②所示，則估計該地區中小學生的平均近視率為（　　）
  

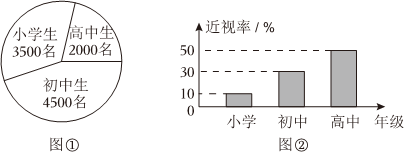
  A．50%

  B．32%

  C．30%

  D．27%
  組卷：43引用：6難度：0.7

  解析

• 6．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的右焦點為F，上頂點為A，若直線AF與圓O：

  x

  2

  +

  y

  2

  =

  3

  a

  2

  16

  相切，則該橢圓的離心率為（　　）

  A． 3 4

  B． 1 2

  C． 3 2

  D． 1 2 或 3 2
  組卷：161引用：2難度：0.5

  解析

• 7．函數

  f

  （

  x

  ）

  =

  -

  x

  +

  b

  （

  x

  +

  c

  ）

  2

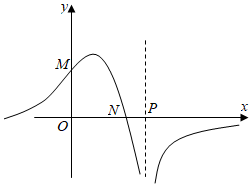  的圖象如圖所示，則下列結論成立的是（　　）

  A．b＜0，c＞0

  B．b＞0，c＞0

  C．b＞0，c＜0

  D．b＜0，c＜0
  組卷：92引用：3難度：0.8

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

• 21．點P在以F₁，F₂為焦點的雙曲線

  E

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）上，已知PF₁⊥PF₂，|PF₁|=2|PF₂|，O為坐標原點．
  （Ⅰ）求雙曲線的離心率e；
  （Ⅱ）過點P作直線分別與雙曲線漸近線相交于P₁，P₂兩點，且

  O

  P

  1

  ?

  O

  P

  2

  =

  -

  27

  4

  ，

  2

  P

  P

  1

  +

  P

  P

  2

  =

  0

  ，求雙曲線E的方程；
  （Ⅲ）若過點Q（m,0）（m為非零常數）的直線l與（2）中雙曲線E相交于不同于雙曲線頂點的兩點M、N，且

  MQ

  =

  λ

  QN

  （λ為非零常數），問在x軸上是否存在定點G，使

  F

  1

  F

  2

  ⊥

  （

  GM

  -

  λ

  GN

  ）

  ？若存在，求出所有這種定點G的坐標；若不存在，請說明理由．
  組卷：72引用：5難度：0.7

  解析

• 22．已知函數f（x）=lnx-e^x+mx,其中m∈R，函數g（x）=f（x）+e^x+1．
  （Ⅰ）當m=1時，求函數f（x）在x=1處的切線方程；
  （Ⅱ）當m=-e時，
  （i）求函數g（x）的最大值；
  （ii）記函數φ（x）=|g（x）|-

  g

  （

  x

  ）

  +

  ex

  -

  1

  x

  -

  1

  2

  ，證明：函數φ（x）沒有零點．
  組卷：113引用：5難度：0.3

  解析