浙教版九年級（上）中考題單元試卷：第2章 二次函數（20）

一、解答題（共30小題）

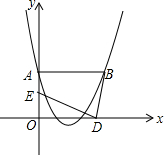• 1．拋物線y=x²+bx+c經過A（0，2），B（3，2）兩點，若兩動點D、E同時從原點O分別沿著x軸、y軸正方向運動，點E的速度是每秒1個單位長度，點D的速度是每秒2個單位長度．
  （1）求拋物線與x軸的交點坐標；
  （2）若點C為拋物線與x軸的交點，是否存在點D，使A、B、C、D四點圍成的四邊形是平行四邊形？若存在，求點D的坐標；若不存在，說明理由；
  （3）問幾秒鐘時，B、D、E在同一條直線上？
  組卷：1819引用：50難度：0.3

  解析

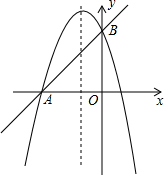• 2．如圖，已知拋物線y=-x²+bx+c與直線AB相交于A（-3，0），B（0，3）兩點．
  （1）求這條拋物線的解析式；
  （2）設C是拋物線對稱軸上的一動點，求使∠CBA=90°的點C的坐標；
  （3）探究在拋物線上是否存在點P，使得△APB的面積等于3？若存在，求出點P的坐標；若不存在，請說明理由．
  組卷：2965引用：54難度：0.1

  解析

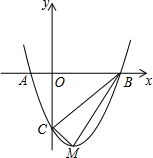• 3．如圖，二次函數y=ax²+bx-3的圖象與x軸交于A（-1，0），B（3，0）兩點，與y軸交于點C．該拋物線的頂點為M．
  （1）求該拋物線的解析式；
  （2）判斷△BCM的形狀，并說明理由；
  （3）探究坐標軸上是否存在點P，使得以點P、A、C為頂點的三角形與△BCM相似？若存在，請直接寫出點P的坐標；若不存在，請說明理由．
  組卷：4532引用：56難度：0.3

  解析

• 4．如圖，在平面直角坐標系中，正方形ABCD和正方形DEFG的邊長分別為2a,2b,點A，D，G在y軸上，坐標原點O為AD的中點，拋物線y=mx²過C，F兩點，連接FD并延長交拋物線于點M．
  （1）若a=1，求m和b的值；
  （2）求

  b

  a

  的值；
  （3）判斷以FM為直徑的圓與AB所在直線的位置關系，并說明理由．
  組卷：1824引用：52難度：0.3

  解析

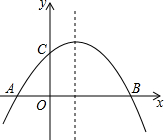• 5．如圖，已知拋物線y=-

  1

  m

  （x+2）（x-m）（m＞0）與x軸相交于點A、B，與y軸相交于點C，且點A在點B的左側．
  （1）若拋物線過點G（2，2），求實數m的值；
  （2）在（1）的條件下，解答下列問題：
  ①求出△ABC的面積；
  ②在拋物線的對稱軸上找一點H，使AH+CH最小，并求出點H的坐標；
  （3）在第四象限內，拋物線上是否存在點M，使得以點A、B、M為頂點的三角形與△ACB相似？若存在，求m的值；若不存在，請說明理由．
  組卷：2727引用：52難度：0.3

  解析

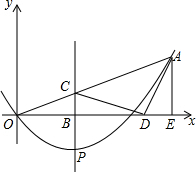• 6．如圖，在平面直角坐標系中，已知拋物線y=ax²+bx的對稱軸為直線x=

  3

  4

  ，且經過點A（2，1），點P是拋物線上的動點，P的橫坐標為m（0＜m＜2），過點P作PB⊥x軸，垂足為B，PB交OA于點C，點O關于直線PB的對稱點為D，連接CD，AD，過點A作AE⊥x軸，垂足為E．
  （1）求拋物線的解析式；
  （2）填空：
  ①用含m的式子表示點C，D的坐標：
  C（

  ，

  ），D（

  ，

  ）；
  ②當m=

  時，△ACD的周長最小；
  （3）若△ACD為等腰三角形，求出所有符合條件的點P的坐標．
  組卷：2162引用：54難度：0.3

  解析

• 7．如圖，已知經過點D（2，-

  3

  ）的拋物線y=

  m

  3

  （x+1）（x-3）（m為常數，且m＞0）與x軸交于點A、B（點A位于B的左側），與y軸交于點C．
  （1）填空：m的值為

   

  ，點A的坐標為

   

  ；
  （2）根據下列描述，用尺規完成作圖（保留作圖痕跡，不寫作法）：連接AD，在x軸上方作射線AE，使∠BAE=∠BAD，過點D作x軸的垂線交射線AE于點E；
  （3）動點M、N分別在射線AB、AE上，求ME+MN的最小值；
  （4）l是過點A平行于y軸的直線，P是拋物線上一點，過點P作l的垂線，垂足為點G，請你探究：是否存在點P，使以P、G、A為頂點的三角形與△ABD相似？若存在，求出點P的坐標；若不存在，說明理由．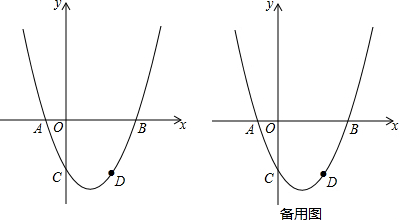
  
  組卷：2177引用：50難度：0.3

  解析

• 8．如圖，在平面直角坐標系中，拋物線y=ax²+bx+

  3

  與x軸交于A（-3，0），B（1，0）兩點．與y軸交于點C，點D與點C關于拋物線的對稱軸對稱．
  （1）求拋物線的解析式，并直接寫出點D的坐標；
  （2）如圖1，點P從點A出發，以每秒1個單位長度的速度沿A→B勻速運動，到達點B時停止運動．以AP為邊作等邊△APQ（點Q在x軸上方），設點P在運動過程中，△APQ與四邊形AOCD重疊部分的面積為S，點P的運動時間為t秒，求S與t之間的函數關系式；
  （3）如圖2，連接AC，在第二象限內存在點M，使得以M、O、A為頂點的三角形與△AOC相似．請直接寫出所有符合條件的點M坐標．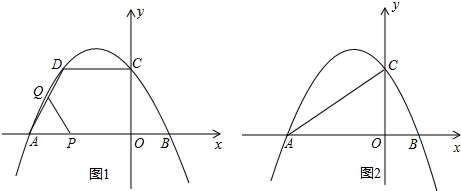
  
  組卷：2612引用：51難度：0.3

  解析

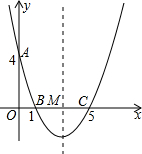• 9．如圖，在直角坐標系中，拋物線經過點A（0，4），B（1，0），C（5，0），其對稱軸與x軸相交于點M．
  （1）求拋物線的解析式和對稱軸；
  （2）在拋物線的對稱軸上是否存在一點P，使△PAB的周長最小？若存在，請求出點P的坐標；若不存在，請說明理由；
  （3）連接AC，在直線AC的下方的拋物線上，是否存在一點N，使△NAC的面積最大？若存在，請求出點N的坐標；若不存在，請說明理由．
  組卷：24323引用：123難度：0.1

  解析

• 10．已知，△ABC在平面直角坐標系中的位置如圖①所示，A點坐標為（-6，0），B點坐標為（4，0），點D為BC的中點，點E為線段AB上一動點，連接DE經過點A、B、C三點的拋物線的解析式為y=ax²+bx+8．
  （1）求拋物線的解析式；
  （2）如圖①，將△BDE以DE為軸翻折，點B的對稱點為點G，當點G恰好落在拋物線的對稱軸上時，求G點的坐標；
  （3）如圖②，當點E在線段AB上運動時，拋物線y=ax²+bx+8的對稱軸上是否存在點F，使得以C、D、E、F為頂點的四邊形為平行四邊形？若存在，請直接寫出點F的坐標；若不存在，請說明理由．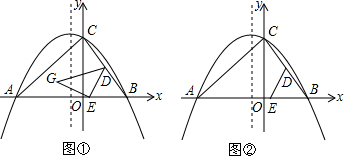
  
  組卷：3780引用：54難度：0.1

  解析

一、解答題（共30小題）

• 29．如圖，在平面直角坐標系中，拋物線y=ax²+bx+2經過點A（-1，0）和點B（4，0），且與y軸交于點C，點D的坐標為（2，0），點P（m,n）是該拋物線上的一個動點，連接CA，CD，PD，PB．
  
  （1）求該拋物線的解析式；
  （2）當△PDB的面積等于△CAD的面積時，求點P的坐標；
  （3）當m＞0，n＞0時，過點P作直線PE⊥y軸于點E交直線BC于點F，過點F作FG⊥x軸于點G，連接EG，請直接寫出隨著點P的運動，線段EG的最小值．
  組卷：2392引用：52難度：0.1

  解析

• 30．如圖1，一條拋物線與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C，且當x=-1和x=3時，y的值相等，直線y=

  15

  8

  x-

  21

  4

  與拋物線有兩個交點，其中一個交點的橫坐標是6，另一個交點是這條拋物線的頂點M．
  （1）求這條拋物線的表達式．
  （2）動點P從原點O出發，在線段OB上以每秒1個單位長度的速度向點B運動，同時點Q從點B出發，在線段BC上以每秒2個單位長度的速度向點C運動，當一個點到達終點時，另一個點立即停止運動，設運動時間為t秒．
  ①若使△BPQ為直角三角形，請求出所有符合條件的t值；
  ②求t為何值時，四邊形ACQP的面積有最小值，最小值是多少？
  （3）如圖2，當動點P運動到OB的中點時，過點P作PD⊥x軸，交拋物線于點D，連接OD，OM，MD得△ODM，將△OPD沿x軸向左平移m個單位長度（0＜m＜2），將平移后的三角形與△ODM重疊部分的面積記為S，求S與m的函數關系式．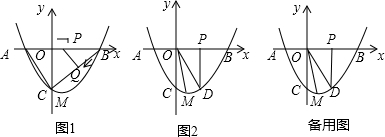
  
  組卷：2617引用：50難度：0.1

  解析