2022-2023學(xué)年廣東省深圳高級(jí)中學(xué)八年級(jí)（下）期末數(shù)學(xué)試卷

一、選擇題。（本大題共10小題，每小題3分，共30分，每個(gè)小題有四個(gè)選項(xiàng)，其中只有一個(gè)是正確的）

• 1．-2023的倒數(shù)是（　　）

  A．-2023

  B．2023

  C．- 1 2023

  D． 1 2023
  組卷：225引用：5難度：0.9

  解析

• 2．圍棋起源于中國，古代稱之為“弈”，至今已有4000多年的歷史．2017年5月，世界圍棋冠軍柯潔與人工智能機(jī)器人AlphaGo進(jìn)行圍棋人機(jī)大戰(zhàn)．截取首局對(duì)戰(zhàn)棋譜中的四個(gè)部分，由黑白棋子擺成的圖案是中心對(duì)稱的是（　　）

  A．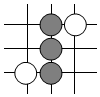

  B．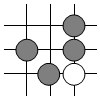

  C．

  D．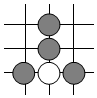
  組卷：2234引用：61難度：0.9

  解析

• 3．ChatGPT是人工智能技術(shù)驅(qū)動(dòng)的自然語言處理工具，它能夠通過理解和學(xué)習(xí)人類的語言來進(jìn)行對(duì)話．初代GPT語言模型的參數(shù)是1.17億個(gè)，而最新模型GPT4的真實(shí)參數(shù)超過1750億，1750億用科學(xué)記數(shù)法表示為（　　）

  A．1.75×108

  B．0.175×109

  C．1.75×1011

  D．0.175×1012
  組卷：152引用：1難度：0.9

  解析

• 4．下列計(jì)算中①（ab²）³=ab⁵；②（3xy²）³=9x³y⁶；③2x³?3x²=6x⁵；④（-c）⁴÷（-c）²=-c² 正確的有（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：322引用：1難度：0.9

  解析

• 5．已知關(guān)于x的不等式組

  3 x - a ≤ 0

  x ≥ 3

  無解，則a的取值范圍是（　　）

  A．a(chǎn)＜9

  B．a(chǎn)＞9

  C．a(chǎn)≥9

  D．a(chǎn)≤9
  組卷：684引用：1難度：0.7

  解析

• 6．某汽車評(píng)測(cè)機(jī)構(gòu)對(duì)市面上多款新能源汽車的0～100km/h的加速時(shí)間和滿電續(xù)航里程進(jìn)行了性能評(píng)測(cè)，評(píng)測(cè)結(jié)果繪制如下，每個(gè)點(diǎn)都對(duì)應(yīng)一款新能源汽車的評(píng)測(cè)數(shù)據(jù)．已知0～100km/h的加速時(shí)間的中位數(shù)是m s,滿電續(xù)航里程的中位數(shù)是n km,相應(yīng)的直線將平面分成了①、②、③、④四個(gè)區(qū)域（直線不屬于任何區(qū)域）．欲將最新上市的兩款新能源汽車的評(píng)測(cè)數(shù)據(jù)對(duì)應(yīng)的點(diǎn)繪制到平面內(nèi)，若以上兩組數(shù)據(jù)的中位數(shù)均保持不變，則這兩個(gè)點(diǎn)可能分別落在（　　）
  

  A．區(qū)域①、②

  B．區(qū)域①、③

  C．區(qū)域①、④

  D．區(qū)域③、④
  組卷：1426引用：5難度：0.6

  解析

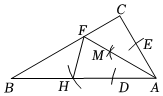• 7．如圖，在Rt△ABC中，∠C=90°，以點(diǎn)A為圓心，任意長為半徑作弧，分別交邊AB，AC于點(diǎn)D，E，分別以點(diǎn)D，E為圓心，大于

  1

  2

  DE的長為半徑作弧，兩弧在∠BAC內(nèi)相交于點(diǎn)M，作射線AM交BC于點(diǎn)F，以點(diǎn)A為圓心，AF的長為半徑作弧，交AB于點(diǎn)H．若∠B=26°，則∠BHF的度數(shù)為（　　）
  ?

  A．100°

  B．106°

  C．110°

  D．120°
  組卷：557引用：5難度：0.7

  解析

三、解答題。（本大題共8題，共55分）

• 22．如圖，在由邊長為1個(gè)單位長度的小正方形組成的網(wǎng)格中建立平面直角坐標(biāo)系，直線l₁：y=2x-5是河岸，河在l₁右側(cè)，l₁左側(cè)的A（2，4）是一個(gè)河鮮冷藏倉庫，B（0，1）是超市．
  （1）現(xiàn)計(jì)劃在河岸l₁上建立一座河鮮加工廠C，加工廠C從倉庫A進(jìn)貨加工，再運(yùn)輸至超市B，請(qǐng)?jiān)趫D中找出加工廠C的位置，使進(jìn)出貨物的運(yùn)輸路徑最短；（僅限在所給網(wǎng)格內(nèi)作圖，不需要說明作圖理由）
  （2）若河的兩岸互相平行，河寬為

  5

  ．
  ①在圖中畫出表示對(duì)面河岸的直線l₂，并直接寫出l₂的解析式；
  ②l₂上有一點(diǎn)D，縱坐標(biāo)為6，l₂右側(cè)有一點(diǎn)E（9，3），線段DE是支流（寬度不計(jì)），支流有豐富多樣的河鮮可以打撈．為支持河鮮產(chǎn)業(yè)發(fā)展，政府計(jì)劃垂直于河的兩岸造橋，漁民在支流處打撈河鮮后裝上貨車，運(yùn)輸河鮮到對(duì)岸的河鮮冷藏倉庫A．請(qǐng)求出l₂上的造橋位置F的坐標(biāo)，以及支流DE上的打撈河鮮位置G的坐標(biāo)，使運(yùn)輸路徑最短．?
  組卷：600引用：2難度：0.4

  解析

• 23．【探索發(fā)現(xiàn)】
  “旋轉(zhuǎn)”是一種重要的圖形變換，圖形旋轉(zhuǎn)過程中蘊(yùn)含著眾多數(shù)學(xué)規(guī)律，以圖形旋轉(zhuǎn)為依托構(gòu)建的解題方法是解決幾何問題的常用方法．如圖1，在正方形ABCD中，點(diǎn)E在AD上，點(diǎn)F在CD上，∠EBF=45°．
  某同學(xué)進(jìn)行如下探索：
  第一步：將△ABE繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°，得到△CBG，且F、C、G三點(diǎn)共線；
  第二步：證明△BEF≌△BGF；
  第三步：得到∠AEB和∠FEB的大小關(guān)系，以及AE、CF、EF之間的數(shù)量關(guān)系；
  請(qǐng)完成第二步的證明，并寫出第三步的結(jié)論．
  【問題解決】
  如圖2，在正方形ABCD中，點(diǎn)P在AD上，且不與A、D重合，將△ABP繞點(diǎn)B順時(shí)針旋轉(zhuǎn)，旋轉(zhuǎn)角度小于90°，得到△A'BP'，當(dāng)P、A′、P′三點(diǎn)共線時(shí)，這三點(diǎn)所在直線與CD交于點(diǎn)Q，要求使用無刻度的直尺與圓規(guī)找到Q點(diǎn)位置，某同學(xué)做法如下：連接AC，與BP交于點(diǎn)O，以O(shè)為圓心，OB為半徑畫圓弧，與CD相交于一點(diǎn)，該點(diǎn)即為所求的點(diǎn)Q．
  請(qǐng)證明該同學(xué)的做法．（前面【探索發(fā)現(xiàn)】中的結(jié)論可直接使用，無需再次證明）
  【拓展運(yùn)用】
  如圖3，在邊長為2的正方形ABCD中，點(diǎn)P在AD上，BP與AC交于點(diǎn)O，過點(diǎn)O作BP的垂線，交AB于點(diǎn)M，交CD于點(diǎn)N，設(shè)AP+AB=x（2≤x≤4），AM=y,直接寫出y關(guān)于x的函數(shù)表達(dá)式．
  ?
  組卷：846引用：1難度：0.5

  解析