2022-2023學年貴州省畢節市威寧縣中水鎮七年級（下）期中數學試卷

一、選擇題（本大題共12個小題，每小題3分，共36分．在每小題給出的四個選項中，只有一項是符合題目要求的，請把正確答案填涂在答題卡上的相應位置處）

• 1．2023⁰的值為（　　）

  A．0

  B．2023

  C．1

  D． 1 2023
  組卷：185引用：4難度：0.9

  解析

• 2．清代詩人袁枚創作了一首詩《苔》：“白日不到處，青春恰自來．苔花如米小，也學牡丹開．”歌頌了苔在惡劣環境下仍有自己的生命意向．若苔花的花粉粒直徑約為0.0000084米，用科學記數法表示為（　　）

  A．0.84×10-5

  B．8.4×10-6

  C．84×10-7

  D．8.4×10-8
  組卷：718引用：17難度：0.5

  解析

• 3．下列計算結果正確的是（　　）

  A．2a3+a3=3a6	B．（-a）2?a3=-a6
  C．（- 1 2 ）-2=4	D．（-2）0=-1
  組卷：7657引用：66難度：0.9

  解析

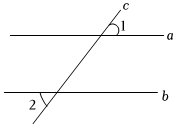• 4．如圖，直線a、b被直線c所截，若a∥b,∠1=40°，則∠2的度數為（　　）

  A．140°

  B．80°

  C．50°

  D．40°
  組卷：52引用：3難度：0.7

  解析

• 5．數學課上老師用雙手形象的表示了“三線八角”圖形，如圖所示（兩大拇指代表被截直線，食指代表截線）．從左至右依次表示（　　）
  

  A．同位角、內錯角、同旁內角

  B．同旁內角、同位角、內錯角

  C．同位角、對頂角、同旁內角

  D．同位角、內錯角、對頂角
  組卷：691引用：5難度：0.5

  解析

• 6．根據科學研究表明，在彈簧的承受范圍內，彈簧掛上物體后會伸長，測得一彈簧的長度y（cm）與所掛的物體的重量x（kg）間有下表的關系：下列說法不正確的是（　　）
  

  x/kg	0	1	2	3	4	5
  y/cm	20	20.5	21	21.5	22	22.5

  A．彈簧不掛重物時的長度為0cm

  B．x與y都是變量，且x是自變量，y是因變量

  C．隨著所掛物體的重量增加，彈簧長度逐漸變長

  D．所掛物體的重量每增加1kg,彈簧長度增加0.5cm
  組卷：1107引用：6難度：0.7

  解析

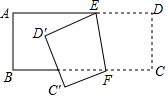• 7．如圖，將長方形ABCD沿直線EF折疊到ED'C'F的位置，若∠DEF=70°，則∠BFC'的度數為（　　）

  A．20°

  B．30°

  C．40°

  D．50°
  組卷：599引用：6難度：0.8

  解析

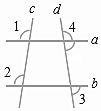• 8．如圖，直線a、b與直線c、d相交，若∠1=∠2，∠3=70°，則∠4的度數是（　　）

  A．35°

  B．70°

  C．90°

  D．110°
  組卷：96引用：2難度：0.7

  解析

三、解答題（本大題共9小題，共98分．解答應在答題卡的相應位置寫出文字說明、證明過程或演算步驟．）

• 24．閱讀與思考
  閱讀下列材料，完成后面的任務：
  

  趙爽“弦圖”與完全平方公式三國時期吳國的數學家趙爽創建了一幅“弦圖”，利用面積法給出了勾股定理的證明．實際上，該“弦圖”與完全平方公式有著密切的關系，如圖2，這是由8個全等的直角邊長分別為a,b,斜邊長為c的三角形拼成的“弦圖”．由圖可知，1個大正方形ABCD的面積=8個直角三角形的面積+1個小正方形PQMN的面積．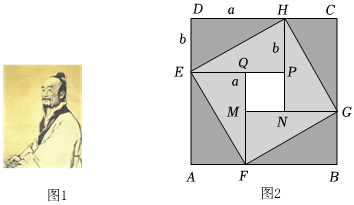

  任務：
  （1）在圖2中，正方形ABCD的面積可表示為

  ，正方形PQMN的面積可表示為

  ．（用含a,b的式子表示）
  （2）根據S_{正方形ABCD}=8S_{直角三角形}+S_{正方形PQMN}，可得（a+b）²，ab,（a-b）²之間的關系為

  ．
  （3）根據（2）中的等量關系，解決問題：已知a+b=5，ab=4，求（a-b）²的值．
  組卷：945引用：5難度：0.6

  解析

• 25．【閱讀與思考】
  如圖，已知AM∥BN，∠A=64°．點P是射線AM上一動點（與點A不重合），BC、BD分別平分∠ABP和∠PBN，分別交射線AM于點C，D．
  【思考與探究】
  （1）①∠ABN的度數是

  ；
  ②∵AM∥BN，∴∠ACB=∠

  ；
  ③∠CBD的度數是

  ；
  【猜想與探究】
  （2）當點P運動時，∠APB與∠ADB之間的數量關系是否隨之發生變化？若不變化，請寫出它們之間的關系，并說明理由；若變化，請寫出變化規律；
  （3）當點P運動到使∠ACB=∠ABD時，∠ABC的度數是多少？
  組卷：593引用：1難度：0.3

  解析