2022-2023學年山西省運城實驗中學七年級（下）期中數學試卷
發布：2024/4/20 14:35:0
一、選擇題（本題共10個小題，每小題3分，共30分，請將每題中唯一正確答案的序號填入題前的方框內）
-
1．（3-π）0=（ ）
組卷：137引用：1難度：0.7 -
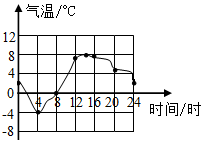2．如圖，是A市某一天的氣溫隨時間變化的情況，則這天的日溫差（最高氣溫與最低氣溫的差）是（ ）組卷：1226引用：23難度：0.6 -
3．下列運算正確的是（ ）
組卷：281引用：5難度：0.9 -
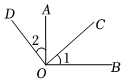4．如圖所示，已知OA⊥OB，OC⊥OD，則圖中∠1=∠2，這是根據（ ）組卷：143引用：4難度：0.7 -
5．中芯國際集成電路制造有限公司，是世界領先的集成電路晶圓代工企業之一，也是中國內地技術最先進、配套最完善、規模最大、跨國經營的集成電路制造企業集團，中芯國際第二代7納米FinFET技術取得了突破性進展，代表了中國大陸自主研發集成電路的最先進水平，1納米=0.000000001米，則7納米用科學記數法表示為（ ）
組卷：204引用：6難度：0.8 -
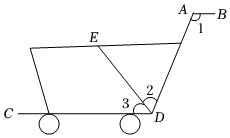6．如圖所示的是超市里購物車的側面示意圖，扶手AB與車底CD平行，∠1=120°，∠2=68°，則∠3的度數是（ ）組卷：138引用：5難度：0.7 -
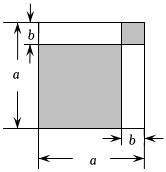7．如圖，邊長為a的正方形分割成兩個正方形和兩個長方形，根據圖中各部分面積之間的關系能驗證的等式是（ ）組卷：523引用：8難度：0.6
三、解答題（共8小題，滿分70分）
-
22．【知識生成】通常，用兩種不同的方法計算同一個圖形的面積，可以得到一個恒等式．
例如：如圖①是一個長為2a,寬為2b的長方形，沿圖中虛線用剪刀將其均分成四個小長方形，然后按圖②的形狀拼成一個正方形．請解答下列問題：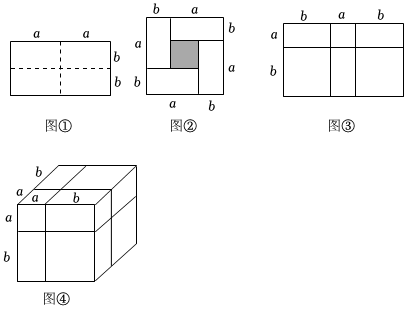
（1）觀察圖②，請你寫出（a+b）2，（a-b）2、ab之間的等量關系是 ；
（2）根據（1）中的等量關系解決如下問題：若x+y=6，xy=5，求（x-y）2的值；
（3）觀察圖③，它可以看成是把一個大長方形分割成小長方形或者小正方形，從中可以得到恒等式：a2+3ab+2b2=；
【知識遷移】類似地，用兩種不同的方法計算同一幾何體的體積，也可以得到一個恒等式．
（4）觀察圖④，它可以看成是把一個大正方體分割成小長方體或小正方體，從中可以得到恒等式：（a+b）3=．組卷：135引用：1難度：0.7 -
23．【閱讀理解】：兩條平行線間的拐點問題經常可以通過作一條直線的平行線進行轉化．
例如：如圖1，MN∥PQ，點C、B分別在直線MN、PQ上，點A在直線MN、PQ之間．問∠CAB，∠MCA，∠PBA之間有何數量關系？請說明理由．
小銘同學發現∠CAB=∠MCA+∠PBA，并給出了部分理由．
如圖1，過點A作AD∥MN，
因為MN∥PQ，AD∥MN，
所以AD∥MN∥PQ，
…；
（1）請將上面的說理過程補充完整；
（2）如圖2，若AB∥CD，∠BEP=160°，∠PFD=129°．則∠EPF= °；
【方法運用】
（3）如圖3，AB∥CD，點P在AB的上方，問∠PEA，∠PFC，∠EPF之間有何數量關系？請說明理由；
【聯想拓展】
（4）如圖4，已知∠EPF=α，∠PEA的平分線和∠PFC的平分線交于點G，請你用含有α的式子表示∠G的度數，直接寫出結果．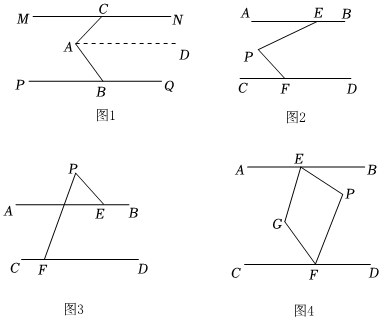
組卷：497引用：2難度：0.7