當前位置：試卷中心 > 試卷詳情

2022年寧夏銀川市金鳳區唐徠回民中學南校區中考數學一模試卷

發布：2024/4/20 14:35:0

一、選擇題（本題共8小題，每小題3分，共24分．在每小題給出的四個選項中只有一個是符合題目要求的）

1．截至北京時間3月8日，全球新冠肺炎確診病例達60840000例，其中60840000用科學記數法表示為（　　）
A．0.6084×10⁷ B．6.084×10⁷ C．0.6084×10⁶ D．60.84×10⁶
組卷：1引用：1難度：0.7
解析
2．下列運算正確的是（　　）
A．x³+x²=x⁵ B．（x+y）²=x²+y²
C．x³÷x=x³ D．（-3x）²=9x²
組卷：83引用：2難度：0.8
解析
3．為了提升學生的人文素養，某校開展了朗誦經典文學作品活動，來自不同年級的30名參賽同學的得分情況如圖所示，這些成績的中位數和眾數分別是（　　）
A．92分，96分 B．94分，96分 C．96分，96分 D．96分，100分
組卷：210引用：6難度：0.7
解析
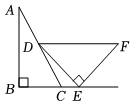4．一副直角三角板如圖放置，點E在邊BC的延長線上，BE∥DF，∠B=∠DEF=90°，則∠CDE的度數為（　　）
A．10° B．15° C．18° D．30°
組卷：124引用：4難度：0.7
解析
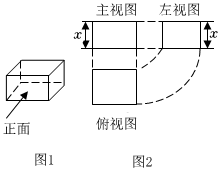5．圖2是圖1中長方體的三視圖，若用S表示面積，S_主=x²+2x,S_左=x²+x,則S_俯=（　　）
A．x²+4x+3 B．2x²+4x C．x²+2x+1 D．x²+3x+2
組卷：75引用：2難度：0.7
解析
6．我國古代數學著作《增刪算法統宗》記載“繩索量竿”問題：“一條竿子一條索，索比竿子長一托．折回索子卻量竿，卻比竿子短一托．“其大意為：現有一根竿和一條繩索，用繩索去量竿，繩索比竿長5尺；如果將繩索對半折后再去量竿，就比竿短5尺．設繩索長x尺，竿長y尺，則符合題意的方程組是（　　）
A．
x
=
y
+
5
1
2
x
=
y
-
5
B．
x
=
y
-
5
1
2
x
=
y
+
5
C．
x
=
y
+
5
2
x
=
y
-
5
D．
x
=
y
-
5
2
x
=
y
+
5
組卷：1800引用：117難度：0.7
解析
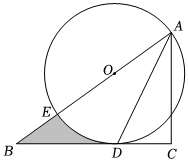7．如圖，在Rt△ABC中，∠C=90°，AC=BC，點O在AB上，經過點A的⊙O與BC相切于點D，交AB于點E，若
CD
=
3
，則圖中陰影部分面積為（　　）
A．3-
π
2
B．3-π C．3-
3
π
4
D．4-
3
π
4
組卷：52引用：2難度：0.5
解析
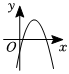8．已知y=ax²+bx+c（a≠0）的圖象如圖，則y=ax+c和y=
b
x
的圖象為（　　）
A． B．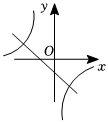
C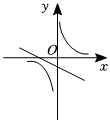． D．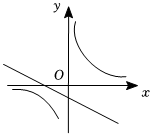
組卷：66引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共4小題，其中23、24題每題8分，25、26題每題10分，共36分）

25．遮陽傘可以遮住灼灼驕陽，站在傘下會涼爽很多，如圖①，把遮陽傘（傘體的截面示意圖為△ABC）用立柱OP固定在地面上的點O處，此時OP垂直于地面OQ，遮陽傘頂點A與P重合．需要遮陽時，向上調節遮陽傘立柱OP上的滑動調節點B，打開支架PD，傘面撐開如圖②，其中，AB'=AC=2m,∠C=30°，D為AB'中點，PD=1m,根據生活經驗，當太陽光線與傘口BC垂直時，遮陽效果最佳．（圖中的虛線就是太陽光線，同一時刻的太陽光線是平行的）
（1）某天上午10點，太陽光線與地面的夾角為60°，如圖③，為使遮陽效果最佳，滑動調節點B，此時立柱PO與支梁PD夾角是多少度？
（2）在（1）的情況下，若遮陽傘落在地面上的陰影近似為以MN為直徑的圓形，如圖④所示，你能求出這個陰影的面積有多大嗎？（提示：過B'作MN的平行線）
（3）如圖⑤，正午時分，太陽光與地面的夾角約為80°，滑動調節點B到B₁，使遮陽效果最佳，此對調節點B滑動的距離約為多少？
（sin50≈0.756，cos50≈0.643，tan50°≈1.192，結果精確到0.01m）
組卷：292引用：1難度：0.3
解析
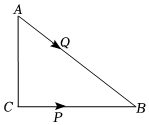26．如圖，△ABC是直角三角形，∠C=90°，AC=6cm,BC=8cm,點P是由C向B移動的一個動點，點Q是由A向B移動的一個動點，已知點P與點Q同時出發，當一個點到達點B時，另一個點就停止移動，設點P的移動速度是每秒1cm,運動時間是t s.
（1）在移動過程中，為了使點P和點Q同時到達點B，求點Q的移動速度；
（2）如果點Q的移動速度是每秒2cm,是否存在某一時刻t,使得AC∥PQ，若存在，求出t,若不存在，說明理由；
（3）如果點Q的移動速度是每秒2cm,用含t的代數式表示△APQ的面積，求當t為何值時，△APQ的面積最大，并求出最大值．
組卷：53引用：2難度：0.2
解析