2023-2024學年黑龍江省哈工大附中高三（上）期中數學試卷

一、單選題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．如圖所示的Venn圖中，集合A={x∈Z|x²+x-2＜0}，B={x∈Z|-1＜x＜5}，則陰影部分表示的集合是（　　）

  A．{0}

  B．{-1，0}

  C．{0，1，2，3，4}

  D．{-1，1，2，3，4}
  組卷：166引用：4難度：0.5

  解析

• 2．已知復數z滿足（1+2i）z=2+i,則|z|=（　　）

  A． 5 5

  B．1

  C． 5

  D．5
  組卷：49引用：3難度：0.9

  解析

• 3．設l,m是兩條不同的直線，α，β，γ是三個不同的平面，下列說法正確的是（　　）

  A．若l∥α，m∥α，則l∥m	B．若l∥α，l∥β，則α∥β
  C．若l⊥α，m⊥α，則l∥m	D．若α⊥γ，β⊥γ，則α∥β
  組卷：504引用：8難度：0.7

  解析

• 4．某保險公司為客戶定制了A，B，C，D，E共5個險種，并對5個險種參保客戶進行抽樣調查，得出如下的統計圖：
  
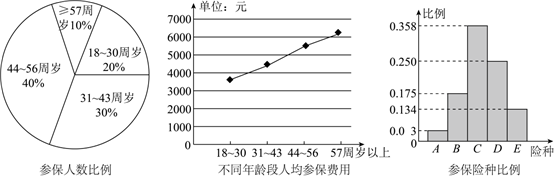
  用該樣本估計總體，以下四個說法錯誤的是（　　）

  A．57周歲以上參保人數最少

  B．18～30周歲人群參保總費用最少

  C．C險種更受參保人青睞

  D．31周歲以上的人群約占參保人群80%
  組卷：174引用：8難度：0.7

  解析

• 5．在數列{a_n}中，若

  a

  1

  =

  2

  ，

  a

  n

  =

  1

  -

  1

  a

  n

  -

  1

  （

  n

  ≥

  2

  ）

  ，則a₂₀₂₃=（　　）

  A．-1

  B． 1 2

  C．2

  D．1
  組卷：193引用：8難度：0.7

  解析

• 6．已知公差不為零的等差數列{a_n}滿足：a₃+a₈=20，且a₅是a₂與a₁₄的等比中項．設數列{b_n}滿足

  b

  n

  =

  1

  a

  n

  a

  n

  +

  1

  （

  n

  ∈

  N

  *

  ）

  ，則數列{b_n}的前n項和S_n為（　　）

  A． 1 2 （ 1 - 1 2 n + 1 ） = n 2 n + 1	B． 1 2 （ 1 + 1 2 n + 1 ） = n 2 n + 1
  C． 1 2 （ 1 - 1 2 n + 1 ） = n 2 n - 1	D． 1 2 （ 1 + 1 2 n + 1 ） = n 2 n - 1
  組卷：222引用：9難度：0.5

  解析

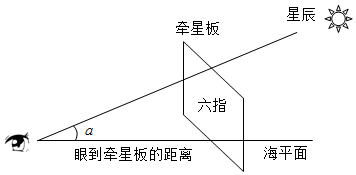• 7．明朝早期，鄭和七下西洋過程中，將中國古代天體測量方面所取得的成就創造性地應用于航海，形成了一套先進的航海技術--“過洋牽星術”．簡單地說，就是通過觀測不同季節、時辰的日月星辰在天空運行的位置和測量星辰在海面以上的高度來判斷方位．其采用的主要工具是牽星板，其由12塊正方形木板組成，最小的一塊邊長約2厘米（稱一指），木板的長度從小到大依次成等差數列，最大的邊長約24厘米（稱十二指）．觀測時，將木板立起，一手拿著木板，手臂伸直，眼睛到木板的距離大約為72厘米，使牽星板與海平面垂直，讓板的下緣與海平面重合，上邊緣對著所觀測的星辰依高低不同替換、調整木板，當被測星辰落在木板上邊緣時所用的是幾指板，觀測的星辰離海平面的高度就是幾指，然后就可以推算出船在海中的地理緯度．如圖所示，若在一次觀測中，所用的牽星板為六指板，則sin2α約為（　　）

  A． 12 35

  B． 12 37

  C． 1 6

  D． 1 3
  組卷：214引用：6難度：0.7

  解析

四、解答題（本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.）

• 21．2023年9月23日第19屆亞運會在中國杭州舉行，其中電子競技第一次列為正式比賽項目．某中學對該校男女學生是否喜歡電子競技進行了調查，隨機調查了男女生人數各200人，得到如下數據：
  

  	男生	女生	合計
  喜歡	120	100	220
  不喜歡	80	100	180
  合計	200	200	400

  （1）根據表中數據，采用小概率值α=0.05的獨立性檢驗，能否認為該校學生對電子競技的喜歡情況與性別有關？
  （2）為弄清學生不喜歡電子競技的原因，采用分層抽樣的方法從調查的不喜歡電子競技的學生中隨機抽取9人，再從這9人中抽取3人進行面對面交流，求“至少抽到一名男生”的概率；
  （3）將頻率視為概率，用樣本估計總體，從該校全體學生中隨機抽取10人，記其中對電子競技喜歡的人數為X，求X的數學期望．
  參考公式及數據：

  χ

  2

  =

  n

  （

  ad

  -

  bc

  ）

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  α	0.15	0.10	0.05	0.025	0.01
  xα	2.072	2.706	3.841	5.024	6.635
  組卷：105引用：6難度：0.6

  解析

• 22．某市為提升中學生的環境保護意識，舉辦了一次“環境保護知識競賽”，分預賽和復賽兩個環節，預賽成績排名前三百名的學生參加復賽．已知共有12000名學生參加了預賽，現從參加預賽的全體學生中隨機地抽取100人的預賽成績作為樣本，得到如圖頻率分布直方圖：
  
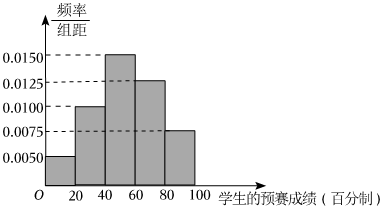
  （1）規定預賽成績不低于80分為優良，若從上述樣本中預賽成績不低于60分的學生中隨機地抽取2人，求至少有1人預賽成績優良的概率，并求預賽成績優良的人數的數學期望；
  （2）由頻率分布直方圖可認為該市全體參加預賽學生的預賽成績Z服從正態分布N（μ，σ²），其中μ可近似為樣本中的100名學生預賽成績的平均值（同一組數據用該組區間的中點值代替），且σ²=362，已知小明的預賽成績為91分，利用該正態分布，估計小明是否有資格參加復賽？
  （3）復賽規則如下：①每人的復賽初始分均為100分；②參賽學生可在開始答題前自行決定答題數量n,每一題都需要“花”掉（即減去）一定分數來獲取答題資格，規定答第k題時“花”掉的分數為0.2k（k=1，2，…，n）；③每答對一題加2分，答錯既不加分也不減分；④答完n題后參賽學生的最終分數即為復賽成績，已知參加復賽的學生甲答對每道題的概率均為0.8，且每題答對與否都相互獨立．若學生甲期望獲得最佳的復賽成績，則他的答題數量n應為多少？
  附：若Z～N（μ，σ²），則P（μ-σ＜Z＜μ+σ）≈0.6827，P（μ-2σ＜Z＜μ+2σ）≈0.9545，P（μ-3σ＜Z＜μ+3σ）≈0.9973；

  362

  ≈

  19

  ．
  組卷：207引用：4難度：0.4

  解析