當前位置：試卷中心 > 試卷詳情

2002年重慶市初中數學競賽試卷（八年級決賽B卷）

發布：2024/10/30 11:30:2

1．計算：
3
-
64
125
×
（
-
2
）
2
+|
（
-
1
）
-
2
+
3
8
|+5^-1的結果是（　　）
A．-
1
2
B．0 C．
2
5
D．
1
2
組卷：120引用：1難度：0.9
解析
2．設a,b,c是△ABC的三條邊，且a³-b³=a²b-ab²+ac²-bc²，則這個三角形是（　　）
A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等腰三角形或直角三角形
組卷：424引用：14難度：0.7
解析
3．已知x可以為任意值，則|2x-1|+|x+2|的最小值是（　　）
A．
5
2
B．5 C．3 D．
3
2
組卷：285引用：2難度：0.9
解析
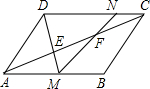4．如圖，平行四邊形ABCD中，AB=24，點E、F三等分對角線AC，DE的延長線交AB于M，MF的延長線交DC于N，則CN等于（　　）
A．8 B．7 C．6 D．4
組卷：129引用：1難度：0.7
解析
5．已知
xy
x
+
y
=1，
yz
y
+
z
=2，
xz
z
+
x
=3，則x的值是（　　）
A．1 B．
12
5
C．
5
12
D．-1
組卷：931引用：8難度：0.7
解析

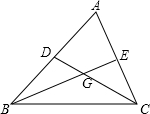14．如圖，△ABC中，∠A=60°，∠ACB的平分線CD和∠ABC的平分線BE交于點G．求證：GE=GD．
組卷：2123引用：2難度：0.1
解析
15．設a₁，a₂，a₃…，a₄₁是任意給定的互不相等的41個正整數．問能否在這41個數中找到6個數，使它們的一個四則運算式的結果（每個數不重復使用）是2002的倍數？如果能，請給出證明；如果不能，請說明理由．
組卷：165引用：1難度：0.1
解析