2022年山東省青島市市南區中考數學三模試卷

一、選擇題（本題滿分24分，共有8道小題，每小題3分）

• 1．一個數的倒數等于-

  1

  2

  ，這個數是（　　）

  A．-2

  B． 1 2

  C．2

  D．- 1 2
  組卷：339引用：7難度：0.9

  解析

• 2．2022年2月15日，世衛組織在新冠肺炎每周流行病學報告中指出，早期研究數據表明，奧密克戎亞變體BA.2毒株更易傳播．奧密克戎直徑約為110納米，1納米=10^-9米，則用科學記數法表示其直徑（單位：米）約為（　　）

  A．1×10-7

  B．0.1×107

  C．1.1×10-7

  D．1.1×107
  組卷：222引用：5難度：0.9

  解析

• 3．下列圖形中，既是中心對稱圖形又是軸對稱圖形的有幾個？（　　）
  

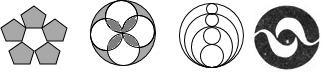
  A．4個

  B．3個

  C．2個

  D．1個
  組卷：175引用：5難度：0.9

  解析

• 4．空心六棱柱螺母按如圖所示位置擺放，則它的左視圖正確的圖形是（　　）

  A．

  B．

  C．

  D．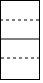
  組卷：302引用：7難度：0.9

  解析

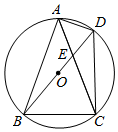• 5．如圖，四邊形ABCD內接于⊙O，連接對角線AC與BD交于點E，且BD為⊙O的直徑，已知∠BDC=40°，∠AEB=110°，則∠ABC=（　　）

  A．65°

  B．70°

  C．75°

  D．80°
  組卷：1350引用：4難度：0.7

  解析

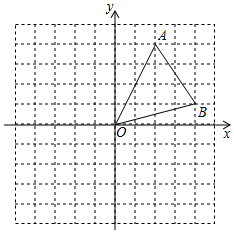• 6．如圖，在平面直角坐標系中，已知點A（2，4），B（4，1），以原點O為位似中心，將△OAB縮小為原來的

  1

  2

  得到△OA₁B₁，當反比例函數y=

  k

  x

  （k≠0）的圖象經過A₁B₁的中點時，k的值為（　　）

  A．30

  B． 15 8

  C．30或-30

  D． 15 8 或- 15 8
  組卷：282引用：4難度：0.7

  解析

• 7．一張矩形紙片ABCD，其中AD=8cm,AB=6cm,先沿對角線BD對折，使點C落在點C′的位置，BC′交AD于點G（圖1）；再折疊一次，使點D與點A重合，得折痕EN，EN交AD于點M（圖2），則EM的長為（　　）
  

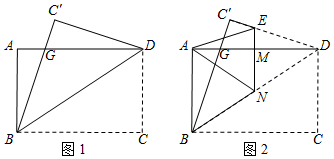
  A．2

  B． 3 2

  C． 2

  D． 7 6
  組卷：1184引用：6難度：0.5

  解析

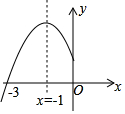• 8．已知二次函數y=-

  1

  4

  x²+bx+c的圖象如圖，則一次函數y=-

  1

  4

  x-2b與反比例函數y=

  c

  x

  在同一平面直角坐標系中的圖象大致是（　　）

  A．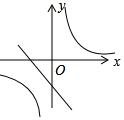

  B．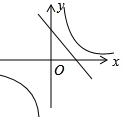

  C．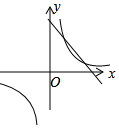

  D．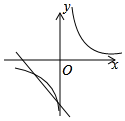
  組卷：1112引用：8難度：0.4

  解析

四、解答題（本題滿分74分，共有9道小題）

• 23．問題提出：如圖1，在矩形ABCD中，點E為AD邊中點，點F為BC邊中點；點G，H為AB邊上與A點最近的兩個n等分點，I，J分別為距離點C、D最近的n等分點．現在分別連接DG、HJ、BI，AF、CE，其中線段AF、線段CE分別與線段DG、HJ、BI相交于點K、L，M，P、O、N，則四邊形KPOL的面積與四邊形ABCD的面積之間存在什么樣的關系？
  
  探究一
  如圖2，點E為AD邊中點，點F為BC邊中點，若點G、H、J、I分別是AB、CD邊上的三等分點，如圖2所示連接各點的線段所圍成的四邊形KPOL的面積與四邊形ABCD的面積的關系是？
  在圖2中，我們對四邊形KPOL面積的探究如下，請你將解題思路填寫完整：
  設S_DEP=a,S_AKG=b,
  ∵EC∥AF
  ∴易證△DEP∽△DAK，且相似比為1：2，得到S_△DAK=4a
  ∵GD∥BI
  ∴易證△AGK∽△ABM，且相似比為1：3，得到S_△ABM=9b
  連接GJ、HI，
  又∵矩形ADJG≌GJIH≌HICB
  連接GJ，HI，∴S_△DAG=4a+b=

  1

  6

  S

  ABCD

  
  連接EF，同理可得S_△ABF=9b+a=

  1

  4

  S

  ABCD

  
  S_ABCD=24a+6b=36b+4a
  a=

  b,S_ABCD=

  b.
  易證平行四邊形KPOL≌平行四邊形LONM，△ADK≌△CBN，△AMB≌△CPD
  ∴S_ABCD=2S_△ADK+2S_△AMB+2S_KPOL
  ∴S_△KPOL=

  b
  ∴S_KPOL=

  S_ABCD
  探究二
  點E為AD邊中點，點F為BC邊中點；若點G、H、J、I分別是AB、CD邊上的四等分點，設S_△DEP=a,S_△AKG=b；則a=

  b,S_KPOL=

  S_ABCD
  問題解決：如圖4，點E為AD邊中點，點F為BC邊中點：點G、H為AB邊上與A點最近的兩個n等分點，I，J分別為距離點C、D最近的n等分點，現在分別連接DG、HJ、BI，AF、CE，其中線段AF、線段CE分別與線段DG、HJ、BI相交于點K、L、M，P、O、N，設S_△DEP=a,S_△AKG=b,則S_KPOL=

  S_ABCD．
  思維拓展：如圖5，點E為AD邊中點，點F為BC邊中點；若點G、H分別是AB邊上離A、B最近的n等分點，點I、J分別是CD邊上離點C、D最近的n等分點，若按照圖5的方式連接矩形ABCD對邊上的點．則S_ANML=

  S_ABCD．
  組卷：345引用：2難度：0.1

  解析

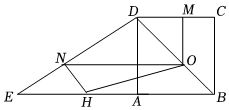• 24．如圖，在正方形ABCD中，AB=6，延長AB到E，使AE=8，動點M從點C出發沿CD方向以每秒1個單位長度的速度向點D運動，同時動點H從點E出發沿EA方向，以每秒2個單位長度的速度向點A勻速運動，過點M作MO∥CB，過點H作HN⊥DE，連接HO，設運動時間為t秒，當其中一個點到達終點后即都停止運動！（0＜t＜4）．
  （1）當HO∥ED時，求t的值；
  （2）連接DH，設四邊形DHOM的面積為S．求S與t之間的函數關系式；
  （3）當點H在∠DMO的角平分線上時，求t的值；
  （4）連接HM，是否存在某一時刻t,使HM與DO互相垂直？若存在，求出t的值；若不存在，說明理由．
  組卷：226引用：2難度：0.3

  解析