2022-2023學年河南省洛陽市宜陽第一高級中學清北班高二（上）第六次月考數學試卷（理科）

一、選擇題（每小題5分，共12小題60分）

• 1．由曲線x²+y²=2|x|+2|y|圍成的圖形的面積為（　　）

  A．8+2π

  B．8+4π

  C．6+4π

  D．6+2π
  組卷：53引用：1難度：0.6

  解析

• 2．已知圓C：x²+y²=1，直線l：x+y+2=0，P為直線l上的動點，過點P作圓C的兩條切線，切點分別為A，B，則直線AB過定點（　　）

  A． （ - 1 2 ，- 1 2 ）

  B．（-1，-1）

  C． （ - 1 2 ， 1 2 ）

  D． （ 1 2 ，- 1 2 ）
  組卷：490引用：4難度：0.5

  解析

• 3．已知圓C₁：x²+y²+4ax+4a²-4=0和圓C₂：x²+y²-2by+b²-1=0只有一條公切線，若a,b∈R且ab≠0，則

  1

  a

  2

  +

  1

  b

  2

  的最小值為（　　）

  A．2

  B．4

  C．8

  D．9
  組卷：231引用：13難度：0.7

  解析

• 4．已知橢圓C₁和雙曲線C₂有相同的焦點F₁和F₂，其中F₂為右焦點，兩曲線在第一象限的交點為P，離心率分別為e₁、e₂，若線段PF₂的垂直平分線經過F₁，則

  1

  e

  1

  +

  1

  e

  2

  =（　　）

  A． 2

  B．2

  C． 3

  D．3
  組卷：319引用：4難度：0.6

  解析

• 5．已知雙曲線Γ：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =1（a＞0，b＞0）的上焦點F（0，c）（c＞0），M是雙曲線下支上的一點，線段MF與圓x²+y²-

  2

  c

  3

  y+

  a

  2

  9

  =0相切于點D，且|MF|=3|DF|，則雙曲線Γ的漸近線方程為（　　）

  A．4x±y=0

  B．x±4y=0

  C．2x±y=0

  D．x±2y=0
  組卷：232引用：9難度：0.7

  解析

• 6．已知拋物線C：y²=2px（p＞0）的焦點為F，A，B為拋物線C上的兩個動點，設AB的中點D到拋物線的準線的距離為d,若|AB|=d,則cos∠AFB的最小值為（　　）

  A．- 1 3

  B．- 1 2

  C． 1 3

  D． 1 2
  組卷：22引用：1難度：0.5

  解析

• 7．圖1是第七屆國際數學教育大會（簡稱ICME7）的會徽圖案，會徽的主體圖案是由如圖2所示的一連串直角三角形演化而成的，其中OA₁=A₁A₂=A₂A₃=…=A₇A₈=1，如果把圖2中的直角三角形繼續作下去，記OA₁，OA₂，…，OA_n的長度構成的數列為{a_n}，由此數列的通項公式為a_n=（　　）
  

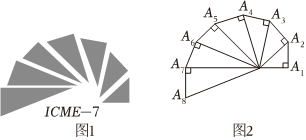
  A．n

  B． n

  C．n+1

  D． n + 1
  組卷：26引用：4難度：0.7

  解析

三、解答題（第17題10分，第18題12分，第19題12分，第20題12分，第21題12分，第22題12分，共6小題70分）

• 21．已知等差數列{a_n}中，

  S

  n

  +

  2

  =

  S

  n

  +

  2

  n

  +

  3

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）求a_n；
  （2）設

  b

  n

  =

  a n + 2 ， n 為奇數 ，

  3 a n ， n 為偶數

  ，求{b_n}的前2n項和T_2n．
  組卷：100引用：4難度：0.6

  解析

• 22．已知橢圓C₁：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  2

  2

  ，且經過點（-

  2

  2

  ，

  3

  2

  ）．
  （Ⅰ）求橢圓C₁的標準方程；
  （Ⅱ）已知拋物線C₂的焦點與橢圓C₁的右焦點重合，過點P（0，-2）的動直線與拋物線C₂相交于A，B兩個不同的點，在線段AB上取點Q，滿足|AP|?|QB|=|AQ|?|PB|，證明：點Q總在定直線上．
  組卷：88引用：2難度：0.5

  解析