2023-2024學年山東省青島市市南區(qū)超銀中學八年級（上）奇點計劃選拔數(shù)學試卷

一、選擇題（每題3分，共24分）

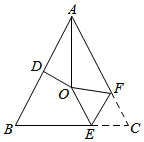• 1．如圖，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分線與AB的垂直平分線交于點O，將∠C沿EF（E在BC上，F(xiàn)在AC上）折疊，點C與點O恰好重合，有如下五個結論：①AO⊥BC；②OD=OE；③△OEF是等邊三角形；④△OEF≌△CEF；⑤∠OEF=54°．則上列說法中正確的個數(shù)是（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：515引用：8難度：0.6

  解析

• 2．對于實數(shù)a、b,定義符號min{a,b}為：當a≥b時，min{a,b}=b；當a＜b時，min{a,b}=a.例如：min{2，-1}=-1，若關于x的函數(shù)y=min{2x-1，-x+3}，則該函數(shù)的最大值是（　　）

  A．1

  B． 4 3

  C． 5 3

  D．2
  組卷：272引用：3難度：0.6

  解析

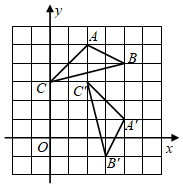• 3．如圖，將△ABC繞點P順時針旋轉得到△A'B'C'，則點P的坐標為（　　）

  A．（1，1）

  B．（1，2）

  C．（1，3）

  D．（1，4）
  組卷：965引用：12難度：0.6

  解析

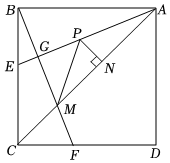• 4．如圖，正方形ABCD的邊長為6，點E，F(xiàn)分別為邊BC，CD上兩點，CF=BE，AE平分∠BAC，連接BF，分別交AE，AC于點G，M，點P是線段AG上的一個動點，過點P作PN⊥AC，垂足為N，連接PM，則下列結論正確的個數(shù)是（　　）
  ①△ABE≌△BCF；
  ②

  AM

  =

  4

  2

  ；
  ③PM+PN的最小值為

  3

  2

  ；
  ④三角形AGM的面積是

  3

  2

  +

  1

  ．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：112引用：1難度：0.5

  解析

• 5．數(shù)論是研究整數(shù)性質的一門理論．它滲透于我們的中小學數(shù)學教材之中，其中整數(shù)的奇偶性也屬于數(shù)論研究內(nèi)容的一部分，偶數(shù)與奇數(shù)的運算性質為：奇數(shù)±奇數(shù)=偶數(shù)；偶數(shù)±偶數(shù)=偶數(shù)；奇數(shù)±偶數(shù)=奇數(shù)；奇數(shù)×奇數(shù)=奇數(shù)；偶數(shù)×偶數(shù)=偶數(shù)；奇數(shù)×偶數(shù)=偶數(shù)．有這樣一道關于整式運算的試題：已知a,b,c為自然數(shù)，使得（a^b-b^c）（b^c-c^a）（c^a-a^b）=11713，請求出a,b,c的值．小明運用整數(shù)的奇偶性進行分析，得出以下結論：
  ①要使等式成立，則（a^b-b^c），（b^c-c^a），（c^a-a^b）三個因式均為奇數(shù)；
  ②可以求出a,b,c的1組解；
  ③可以求出a,b,c的6組解；
  ④沒有符合條件的自然數(shù)a,b,c.
  以上結論正確的個數(shù)為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：148引用：2難度：0.5

  解析

• 6．化簡

  1

  8

  +

  11

  +

  1

  11

  +

  14

  +

  1

  14

  +

  17

  +

  1

  17

  +

  20

  +

  1

  20

  +

  23

  +

  1

  23

  +

  26

  +

  1

  26

  +

  29

  +

  1

  29

  +

  32

  的結果是（　　）

  A．1

  B． 2 2 3

  C． 2 2

  D． 4 2
  組卷：817引用：3難度：0.9

  解析

• 7．10個人圍成一圈做游戲．游戲的規(guī)則是：每個人心里都想一個數(shù)，并把自己想的數(shù)告訴與他相鄰的兩個人，然后每個人將與他相鄰的兩個人告訴他的數(shù)的平均數(shù)報出來，若報出來的數(shù)如圖所示，則報出來的數(shù)是3的人心里想的數(shù)是（　　）

  A．2

  B．-2

  C．4

  D．-4
  組卷：1275引用：12難度：0.3

  解析

• 8．已知關于x,y的方程組

  x - 3 y = 4 - t

  x + y = 3 t

  ，其中-3≤t≤1，給出下列結論：
  ①

  x = 1

  y = - 1

  是方程組的解；
  ②若x-y=3，則t=-2；
  ③若M=2x-y-t,則M的最小值為-3；
  ④若y≥-1時，則0≤x≤3；
  其中正確的有（　　）

  A．①②

  B．①③

  C．①②③

  D．①③④
  組卷：1165引用：5難度：0.4

  解析

三、解答題（每題8分，共40分）

• 24．《見微知著》讀到：從一個簡單的經(jīng)典問題出發(fā)，從特殊到一般，由簡單到復雜：從部分到整體，由低維到高維，知識與方法上的類比是探索發(fā)展重要途徑，是思想閥門發(fā)現(xiàn)新問題、結論的重要方法．
  閱讀材料一：利用整體思想解題，運用代數(shù)式的恒等變形，使不少依照常規(guī)思路難以解決的問題找到簡便解決方法，常用的途徑有：（1）整體觀察；（2）整體設元；（3）整體代入；（4）整體求和等．
  例如：ab=1，求證：

  1

  1

  +

  a

  +

  1

  1

  +

  b

  =

  1

  
  證明：左邊=

  1

  1

  +

  a

  +

  1

  1

  +

  b

  =

  ab

  ab

  +

  a

  +

  1

  1

  +

  b

  =

  b

  1

  +

  b

  +

  1

  1

  +

  b

  =

  1

  
  波利亞在《怎樣解題》中指出：“當你找到第一個藤菇或作出第一個發(fā)現(xiàn)后，再四處看看，他們總是成群生長”類似問題，我們有更多的式子滿足以上特征：
  閱讀材料二
  基本不等式

  a

  +

  b

  2

  ≥

  ab

  （a＞0，b＞0），當且僅當a=b時等號成立，它是解決最值問題的有力工具．
  例如：在x＞0的條件下，當x為何值時，

  x

  +

  1

  x

  有最小值，最小值是多少？
  解：∵x＞0，

  1

  x

  ＞

  0

  ，∴

  x

  +

  1

  x

  2

  ≥

  x

  ?

  1

  x

  =

  1

  =

  1

  ，即

  x

  +

  1

  x

  ≥

  2

  ，
  當且僅當

  x

  =

  1

  x

  ，即x=1時，

  x

  +

  1

  x

  有最小值，最小值為2，
  請根據(jù)閱讀材料解答下列問題：
  （1）已知ab=1，求下列各式的值：
  ①

  1

  1

  +

  a

  2

  +

  1

  1

  +

  b

  2

  =

  ；
  ②

  1

  1

  +

  a

  n

  +

  1

  1

  +

  b

  n

  =

  ；
  （2）若abc=1，求

  5

  a

  ab

  +

  a

  +

  1

  +

  5

  b

  bc

  +

  b

  +

  1

  +

  5

  c

  ca

  +

  c

  +

  1

  的值；
  （3）已知長方形的面積為9，求此長方形周長的最小值；
  （4）若正數(shù)a、b滿足ab=1，求

  M

  =

  1

  1

  +

  a

  +

  1

  1

  +

  2

  b

  的最小值．
  組卷：693引用：2難度：0.3

  解析

• 25．問題提出
  （1）如圖①，在Rt△ABC中，∠B=90°，AB=3，BC=4．若點P是邊AC上一點，則BP的最小值為

  ；
  問題探究
  （2）如圖②，在Rt△ABC中，∠B=90°，AB=BC=2，點E是BC的中點．若點P是邊AC上一點，試求PB+PE的最小值；
  問題解決
  （3）某市一濕地公園內(nèi)有一條四邊形ABCD型環(huán)湖路，如圖③所示．已知AD=2000米，CD=1000米，∠A=60°，∠B=90°，∠C=150°．為了進一步提升服務休閑功能，滿足市民游園和健身需求，現(xiàn)要修一條由CE，EF，F(xiàn)C連接而成的步行景觀道，其中，點E，F(xiàn)分別在邊AB，AD上．為了節(jié)省成本，要使所修的這條步行景觀道最短，即CE+EF+FC的值最小，求此時BE，DF的長．（路面寬度忽略不計）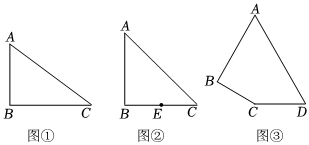
  
  組卷：1797引用：6難度：0.1

  解析