2022-2023學年北京市中關村中學高二（下）期中數學試卷

一、選擇題（本大題共10小題，每小題4分，共40分.在每題列出的四個選項中，選出最符合題目要求的一項.）

• 1．已知等差數列{a_n}中，a₁=4，a₄+a₆=10，那么a₂+a₄=（　　）

  A． 17 2

  B．9

  C．10

  D．24
  組卷：526引用：2難度：0.8

  解析

• 2．已知各項均為正數的等比數列{a_n}滿足

  a

  1

  a

  3

  =

  1

  4

  ，a₂a₄=1，則a₆=（　　）

  A．2

  B．4

  C．8

  D．16
  組卷：248引用：2難度：0.7

  解析

• 3．某城市的汽車牌照號碼由2個英文字母后接4個數字組成，其中4個數字互不相同的牌照號碼共有（　　）

  A． （ C 1 26 ） 2 A 4 10	B． A 2 26 A 4 10 個
  C． （ C 1 26 ） 2 1 0 4 個	D． A 2 26 1 0 4 個
  組卷：426引用：26難度：0.9

  解析

• 4．下列給出四個求導運算：
  ①（x-

  1

  x

  ）′=

  x

  2

  -

  1

  x

  2

  ；②（xe^x）′=e^x（x+1）；③（

  sinx

  2

  ）

  ′

  =

  cosx

  4

  ；④（x²-x-lnx）′=

  （

  x

  -

  1

  ）

  （

  2

  x

  +

  1

  ）

  x

  ．
  其中運算結果正確的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：432引用：3難度：0.7

  解析

• 5．如果把二次函數f（x）=ax²+bx+c與其導函數f′（x）的圖象畫在同一個坐標系中．則下面四組圖中一定錯誤的是（　　）

  A．

  B．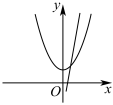

  C．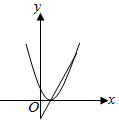

  D．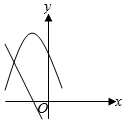
  組卷：17引用：3難度：0.9

  解析

• 6．已知等差數列{a_n}，則“a₂＞a₁”是“數列{a_n}為單調遞增數列”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：189引用：8難度：0.9

  解析

• 7．在各項均為正數的等比數列{a_n}中，a₁a₁₁+2a₅a₉+a₃a₁₃=25，則a₁a₁₃的最大值是（　　）

  A．25

  B． 25 4

  C．5

  D． 2 5
  組卷：643引用：4難度：0.7

  解析

三、解答題（本大題共6小題，共85分.解答應寫出文字說明，證明過程或演算步驟.）

• 20．已知函數f（x）=ln（ax）-（a+1）x,其中a∈R且a≠0．
  （1）當a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）求函數f（x）的單調區間；
  （3）若函數f（x）沒有零點，求實數a的取值范圍．
  組卷：207引用：2難度：0.6

  解析

• 21．若無窮數列{a_n}滿足：只要a_p=a_q（p,q∈N^*），必有a_p+1=a_q+1，則稱{a_n}具有性質P．
  （1）若{a_n}具有性質P，且a₁=1，a₂=2，a₄=3，a₅=2，a₆+a₇+a₈=21，求a₃；
  （2）若無窮數列{b_n}是等差數列，無窮數列{c_n}是公比為正數的等比數列，b₁=c₅=1；b₅=c₁=81，a_n=b_n+c_n，判斷{a_n}是否具有性質P，并說明理由；
  （3）設{b_n}是無窮數列，已知a_n+1=b_n+sina_n（n∈N^*），求證：“對任意a₁，{a_n}都具有性質P”的充要條件為“{b_n}是常數列”．
  組卷：1921引用：12難度：0.1

  解析