2022-2023學年浙江省杭州師大附中高二（上）期末數學試卷

一、單項選擇（共8題，每小題5分；滿分40分）

• 1．空間兩點A，B的坐標分別為（1，2，3），（-1，-2，3），則A，B兩點的位置關系是（　　）

  A．關于x軸對稱	B．關于xOy平面對稱
  C．關于z軸對稱	D．關于原點對稱
  組卷：101引用：4難度：0.8

  解析

• 2．若把數據x₁，x₂，x₃，?，x₂₀₂₂，改變為x₁-2，x₂-2，x₃-2，?，x₂₀₂₂-2，則它們的（　　）

  A．平均數與方差均不改變

  B．平均數改變，方差保持不變

  C．平均數不變，方差改變

  D．平均數與方差均改變
  組卷：139引用：3難度：0.7

  解析

• 3．若直線l的一個方向向量為

  v

  =

  （

  -

  2

  ，-

  2

  ，-

  4

  ）

  ，平面α的一個法向量為

  n

  =

  （

  1

  ，

  1

  ，

  2

  ）

  ，則直線l與平面α的位置關系是（　　）

  A．垂直	B．平行
  C．相交但不垂直	D．平行或線在面內
  組卷：272引用：5難度：0.7

  解析

• 4．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  25

  =1（a＞5）的兩個焦點為F₁、F₂，且|F₁F₂|=8．弦AB過點F₁，則△ABF₂的周長為（　　）

  A．10

  B．20

  C．2 41

  D．4 41
  組卷：387引用：46難度：0.7

  解析

• 5．“中國剩余定理”講的是一個關于整除的問題，現有這樣一個問題：將正整數中能被3除余2且被7除余2的數按由小到大的順序排成一列，構成數列{a_n}，則a₆=（　　）

  A．103

  B．107

  C．109

  D．105
  組卷：128引用：4難度：0.7

  解析

• 6．拋物線C₁：y²=4x和圓C₂：（x-1）²+y²=1，直線l經過C₁的焦點F，依次交C₁，C₂于A，B，C，D四點，則

  AB

  ?

  CD

  的值為（　　）

  A． 3 4

  B．1

  C．2

  D．4
  組卷：276引用：7難度：0.5

  解析

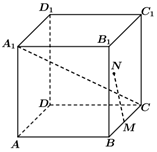• 7．已知棱長為1的正方體ABCD-A₁B₁C₁D₁，M為BC中點，N為平面DCC₁D上的動點，若MN⊥A₁C，則三棱錐N-AA₁D的體積最小值為（　　）

  A． 1 10

  B． 1 12

  C． 1 14

  D． 1 16
  組卷：128引用：2難度：0.7

  解析

四、解答題（共6題，滿分70分）

• 21．如圖，等腰梯形ABCD中，AD∥BC，

  AB

  =

  BC

  =

  CD

  =

  1

  2

  AD

  ，現以AC為折痕把△ABC折起，使點B到達點P的位置，且PA⊥CD．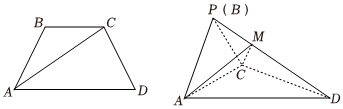
  
  （1）證明：CD⊥平面PAC；
  （2）若M為PD上一點，且三棱錐D-ACM的體積是三棱錐P-ACM體積的2倍，求平面PAC與平面ACM夾角的余弦值．
  組卷：186引用：4難度：0.5

  解析

• 22．已知拋物線y²=4

  3

  x的準線過橢圓E的左焦點，且橢圓E的一個焦點與短軸的兩個端點構成一個正三角形：
  （1）求橢圓E的方程；
  （2）直線y=

  1

  2

  交橢圓E于A，B兩點，點P在線段AB上移動，連接OP交橢圓于M，N兩點，過P作MN的垂線交x軸于Q，求△MNQ面積的最小值．
  組卷：170引用：5難度：0.5

  解析