2023年四川省成都市樹德中學自主招生數學模擬試卷

一、單選題

• 1．下列判斷正確的是（　　）

  A． 5 - 1 2 ＜0.5	B．若ab=0，則a=b=0
  C． a b = a b	D． 8 與 2 是同類二次根式
  組卷：163引用：3難度：0.6

  解析

• 2．下列四個運算中，只有一個是正確的．這個正確運算的序號是（　　）
  ①3⁰+3^-1=-3；②

  5

  -

  2

  =

  3

  ；③（2a²）³=8a⁵；④-a⁸÷a⁴=-a⁴．

  A．①

  B．②

  C．③

  D．④
  組卷：817引用：4難度：0.8

  解析

• 3．如圖1，將一個邊長為m的正方形紙片剪去兩個小長方形得到一個如圖2所示的圖形，再將剪下的兩個小長方形拼成如圖3所示的一個新的長方形，則圖3中的長方形的周長為（　　）
  

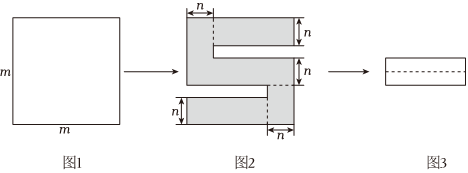
  A．2m-3n

  B．4m-8n

  C．2m-4n

  D．4m-10n
  組卷：686引用：4難度：0.7

  解析

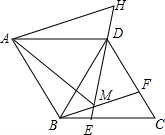• 4．如圖，在菱形ABCD中，AB=BD，點E、F分別在BC、CD上，且BE=CF，連接BF、DE交于點M，延長ED到H使DH=BM，連接AM，AH，則以下四個結論：
  ①△BDF≌△DCE；②∠BMD=120°；③△AMH是等邊三角形；④S_{四邊形ABMD}=

  3

  4

  AM²．
  其中正確結論的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：3576引用：16難度：0.7

  解析

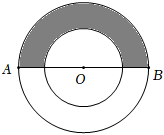• 5．如圖，圓環中大圓的半徑為r,小圓的半徑為

  r

  2

  ，AB為大圓的直徑，則陰影部分的面積為（　　）

  A． π r 2 4

  B． 3 π r 2 4

  C． π r 2 8

  D． 3 π r 2 8
  組卷：622引用：4難度：0.6

  解析

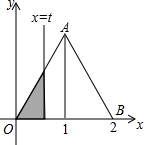• 6．如圖，在直角坐標系的第一象限內，△AOB是邊長為2的等邊三角形，設直線l：x=t（0≤t≤2）截這個三角形所得位于直線左側的圖形（陰影部分）的面積為s,則s關于t的大致圖象是（　　）

  A．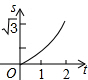

  B．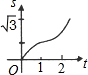

  C．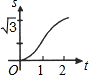

  D．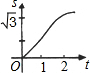
  組卷：162引用：2難度：0.9

  解析

• 7．在一個不透明的袋子里裝有2個紅球和1個白球，它們除顏色外都相同，從中摸出一個球，放回攪勻后，再摸出一個球．兩次都摸到紅球的概率是（　　）

  A． 1 3

  B． 2 3

  C． 2 9

  D． 4 9
  組卷：178引用：4難度：0.6

  解析

三、解答題

• 21．閱讀下列兩則材料，回答問題
  材料一：我們將（

  a

  +

  b

  ）與（

  a

  -

  b

  ）稱為一對“對偶式”
  因為（

  a

  +

  b

  ）（

  a

  -

  b

  ）=（

  a

  ）²-（

  b

  ）²=a-b,所以構造“對偶式”相乘可以有效地將（

  a

  +

  b

  ）和（

  a

  -

  b

  ）中的“

  ”去掉
  例如：已知

  25

  -

  x

  -

  15

  -

  x

  =2，求

  25

  -

  x

  +

  15

  -

  x

  的值．
  解：（

  25

  -

  x

  -

  15

  -

  x

  ）×（

  25

  -

  x

  +

  15

  -

  x

  ）=（25-x）-（15-x）=10
  ∵

  25

  -

  x

  -

  15

  -

  x

  =2，
  ∴

  25

  -

  x

  +

  15

  -

  x

  =5
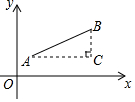
  材料二：如圖，點A（x₁，y₁），點B（x₂，y₂），以AB為斜邊作Rt△ABC，
  則C（x₂，y₁），于是AC=|x₁-x₂|，BC=|y₁-y₂|，所以
  AB=

  （

  x

  1

  -

  x

  2

  ）

  2

  +

  （

  y

  1

  -

  y

  2

  ）

  2

  ．
  反之，可將代數式

  （

  x

  1

  -

  x

  2

  ）

  2

  +

  （

  y

  1

  -

  y

  2

  ）

  2

  的值看作點（x₁，y₁）到點（x₂，y₂）的距離．例如
  

  x

  2

  -

  2

  x

  +

  y

  2

  +

  2

  y

  +

  2

  =

  （

  x

  2

  -

  2

  x

  +

  1

  ）

  +

  （

  y

  2

  +

  2

  y

  +

  1

  ）

  =

  （

  x

  -

  1

  ）

  2

  +

  （

  y

  +

  1

  ）

  2

  =

  （

  x

  -

  1

  ）

  2

  +

  [

  y

  -

  （

  -

  1

  ）

  ]

  2

  ．
  所以可將代數式

  x

  2

  -

  2

  x

  +

  y

  2

  +

  2

  y

  +

  2

  的值看作點（x,y）到點（1，-1）的距離．
  （1）利用材料一，解關于x的方程：

  20

  -

  x

  -

  4

  -

  x

  =2，其中x≤4；
  （2）①利用材料二，求代數式

  x

  2

  -

  2

  x

  +

  y

  2

  -

  16

  y

  +

  65

  +

  x

  2

  +

  4

  x

  +

  y

  2

  -

  4

  y

  +

  8

  的最小值，并求出此時y與x的函數關系式，寫出x的取值范圍；
  ②將①所得的y與x的函數關系式和x的取值范圍代入y=

  2

  x

  2

  +

  5

  x

  +

  12

  +

  2

  x

  2

  +

  3

  x

  +

  6

  中解出x,直接寫出x的值．
  組卷：1229引用：4難度：0.6

  解析

• 22．如圖，已知直線y=2x+2與拋物線y=ax²+bx+c相交于A，B兩點，點A在x軸上，點B在y軸上，點C（3，0）在拋物線上．
  
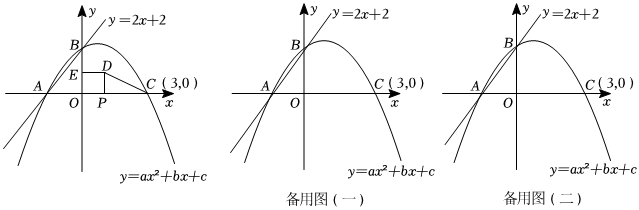
  （1）求該拋物線的表達式；
  （2）正方形OPDE的頂點O為直角坐標系原點，頂點P在線段OC上，頂點E在y軸正半軸上，若△AOB與△DPC全等，求點P的坐標；
  （3）在條件（2）下，點Q是線段CD上的動點（點Q不與點D重合），將△POD沿PQ所在的直線翻折得到△POD′，連接AD′，求AD′長度的取值范圍．
  組卷：508引用：3難度：0.1

  解析