當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省蘇州市太倉一中八年級（下）段考數學試卷（4月份）

發布：2024/11/13 13:0:2

一、選擇題（本大題共10小題，每小題3分，共30分）

1．下列醫療或救援標識中是中心對稱圖形的是（　　）
A． B． C． D．
組卷：134引用：3難度：0.9
解析
2．為了調查市一中學生的視力情況，在全校的2700名學生中隨機抽取了100名學生，下列說法正確的是（　　）
A．此次調查屬于全面調查
B．樣本容量是100
C．1000名學生是總體
D．被抽取的每一名學生稱為個體
組卷：90引用：1難度：0.9
解析

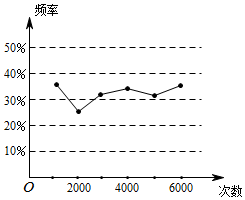3．如圖為某一試驗結果的頻率隨試驗次數變化的趨勢圖，則不符合該圖的試驗是（　　）

A．擲一枚骰子，出現點數不超過2

B．擲一枚硬幣，出現正面朝上

C．從裝有2個黑球、1個白球的布袋中，隨機摸出一球為白球

D．從分別標有數字1-9的九張卡片中，隨機抽取一張卡片，所標記的數字大于6

組卷：170引用：1難度：0.7

解析

4．要使分式
1
x
+
1
有意義，則x應滿足的條件是（　　）
A．x≠1 B．x≠-1 C．x≠0 D．x＞1
組卷：448引用：89難度：0.9
解析
5．已知點M（-2，3）在雙曲線y=
k
x
上，則下列各點一定在該雙曲線上的是（　　）
A．（3，-2） B．（-2，-3） C．（2，3） D．（3，2）
組卷：627引用：13難度：0.9
解析
6．化簡
a
2
-
b
2
a
2
+
ab
的結果為（　　）
A．
a
-
b
2
a
B．
a
-
b
a
C．
a
+
b
a
D．
a
-
b
a
+
b
組卷：1648引用：15難度：0.9
解析
7．已知雙曲線y=
k
x
（k＜0）上有兩點A（x₁，y₁）和B（x₂，y₂），且x₂＞x₁＞0，則y₁-y₂的值是（　　）
A．正數 B．非負數 C．負數 D．零
組卷：48引用：2難度：0.9
解析
8．若方程
m
x
-
4
-
1
-
x
4
-
x
=
0
有增根，則m的值是（　　）
A．1 B．-1 C．3 D．-3
組卷：218引用：8難度：0.7
解析
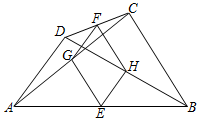9．如圖，在四邊形ABCD中，AB=8，BC=5，CD=3，DA=4，其中E，F，G，H分別是AB，CD，AC，BD的中點，則四邊形EHFG的周長為（　　）
A．10 B．9 C．8 D．7
組卷：287引用：5難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共10小題，共76分，應寫出必要的計算過程、推理步驟或文字說明）

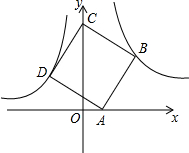27．如圖，點B（3，3）在雙曲線y=
k
x
（x＞0）上，點D在雙曲線y=-
4
x
（x＜0）上，點A和點C分別在x軸，y軸的正半軸上，且點A，B，C，D構成的四邊形為正方形．
（1）求k的值及點A的坐標．
（2）求出對角線BD的長；
（3）若取正方形ABCD各邊的中點E、F、G、H，則中點四邊形EFGH的形狀是
（選填一種特殊平行四邊形的名稱），它的面積是
．
組卷：130引用：2難度：0.7
解析
28．市一中某數學興趣小組利用正方形硬紙片開展了一次活動，請認真閱讀下面的探究片段，完成提出的問題．四邊形ABCD是邊長為3的正方形，點E是射線BC上的動點，∠AEF=90°，且EF交正方形外角的平分線CF于點F．【探究1】當點E是BC中點時，如圖1，發現AE=EF，這需要證明AE與EF所在的兩個三角形全等，但△ABE與△FCE顯然不全等，考慮到點E是BC的中點，取AB的中點H，連接EH，證明△AHE與△ECF全等即可．（無需證明）

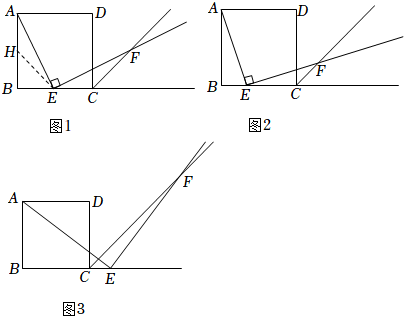
【探究2】（1）如圖2，如果把“點E是BC的中點”改成“點E是邊BC上（不與點B、C重合）的任意一點”，其他條件不變，那么結論“AE=EF”仍然成立嗎？如果成立，寫出證明過程，如果不成立，也請說明理由．
（2）如圖3，如果點E是邊BC延長線上的任意一點，其他條件不變，請你畫出圖象，并判斷“AE=EF”是否成立？
（填“是”或“否”），如果是，請簡述一下輔助線的作法；如果否，也請說明理由．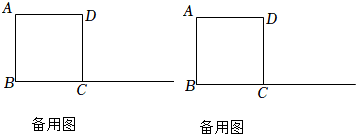

【探究3】連接AF交直線CD于點I，連接EI，試探究線段BE，EI，ID之間的數量關系，請在備用圖中作出圖形并直接寫出結論．
【探究4】當CE=2時，此時△EIF的面積為
．
組卷：425引用：2難度：0.1
解析