當(dāng)前位置：試卷中心 > 試卷詳情

2021-2022學(xué)年海南省海口一中高一（下）期中數(shù)學(xué)試卷（A卷）

發(fā)布：2024/12/31 18:30:3

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

1．已知集合A={x|x＜4}，B={0，1，2，3，4}，則A∩B=（　　）
A．{0，1，2} B．{1，2，3} C．{2，3} D．{0，1，2，3}
組卷：57引用：4難度：0.8
解析
2．b＞a+1是3^b＞3^a的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：187引用：3難度：0.9
解析
3．若一個平面圖形的直觀圖是邊長為2的正三角形，則該平面圖形的面積為（　　）
A．
6
4
B．
2
6
C．
2
4
D．
2
2
組卷：305引用：3難度：0.8
解析
4．已知f（x）為定義在R上的偶函數(shù)，當(dāng)x≤0時，f（x）=2^x，則f（x）的值域?yàn)椋ā　。?/h2>
A．[1，+∞） B．（0，1） C．（0，1] D．（-∞，1]
組卷：98引用：3難度：0.9
解析
5．已知函數(shù)f（x）=2^x-
2
x
-a的一個零點(diǎn)在區(qū)間（1，2）內(nèi)，則實(shí)數(shù)a的取值范圍是（　　）
A．（1，3） B．（1，2） C．（0，3） D．（0，2）
組卷：1292引用：70難度：0.7
解析
6．已知
sin
（
π
6
+
α
）
=
-
3
3
，則
cos
（
2
π
3
-
2
α
）
=（　　）
A．
-
2
3
B．
-
1
3
C．
2
3
D．
1
3
組卷：153引用：4難度：0.7
解析
7．圣?索菲亞教堂（英語：SAINT SOPHIA CATHEDRAL）坐落于中國黑龍江省，是一座始建于1907年拜占庭風(fēng)格的東正教教堂，距今已有114年的歷史，為哈爾濱的標(biāo)志性建筑.1996年經(jīng)國務(wù)院批準(zhǔn)，被列為第四批全國重點(diǎn)文物保護(hù)單位，是每一位到哈爾濱旅游的游客拍照打卡的必到景點(diǎn)．其中央主體建筑集球，圓柱，棱柱于一體，極具對稱之美，可以讓游客從任何角度都能領(lǐng)略它的美．小明同學(xué)為了估算索菲亞教堂的高度，在索菲亞教堂的正東方向找到一座建筑物AB，高為（
15
3
-
15
）m,在它們之間的地面上的點(diǎn)M（B，M，D三點(diǎn)共線）處測得樓頂A，教堂頂C的仰角分別是15°和60°，在樓頂A處測得塔頂C的仰角為30°，則小明估算索菲亞教堂的高度為（　　）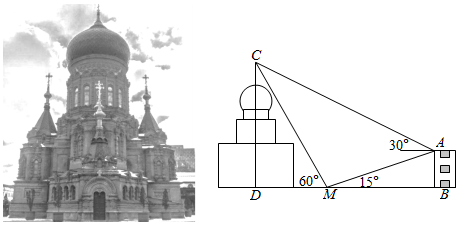
A．20m B．30m C．
20
3
m D．
30
3
m
組卷：360引用：21難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題；本題共6小題，共70分。解答應(yīng)寫出文字說明，證明過程或演算步驟.

21．已知函數(shù)
f
（
x
）
=
1
x
-
1
，
0
＜
x
＜
1
（
x
-
1
）
2
，
x
≥
1
．
（1）當(dāng)0＜a＜b,且f（a）=f（b）時，求
（
1
a
）
2
+（b-1）²的取值范圍；
（2）是否存在正實(shí)數(shù)a,b（a＜b），使得函數(shù)y=f（x）在[a,b]上的取值范圍是[a-1，b-1]．若存在，則求出a,b的值；若不存在，請說明理由．
組卷：111引用：3難度：0.4
解析
22．已知函數(shù)g（x）=sinx,將g（x）的圖象各點(diǎn)橫坐標(biāo)縮短到原來的
1
2
，縱坐標(biāo)伸長到原來的2倍，然后再將所得函數(shù)圖象向左平移
π
6
個單位后得到函數(shù)f（x）的圖象．
（1）求f（x）的解析式；
（2）方程f（x）-2n+1=0在
[
0
，
π
2
]
上有且只有一個解，求實(shí)數(shù)n的取值范圍；
（3）實(shí)數(shù)m滿足對任意x₁∈[-1，1]，都存在x₂∈R，使得
4
x
1
+
4
-
x
1
+
m
（
2
x
1
-
2
-
x
1
）
-
3
＜
f
（
x
2
）
成立，求m的取值范圍．
組卷：168引用：2難度：0.5
解析