當前位置：試卷中心 > 試卷詳情

2023-2024學年陜西省西安市新城區五環中學八年級（上）第一次月考數學試卷

發布：2024/9/21 0:0:8

一、選擇題（共8小題，每小題3分，計24分.每小題只有一個選項是符合題意的）

1．要使
x
-
2
有意義，則x的值可以是（　　）
A．0 B．-1 C．-2 D．2
組卷：870引用：12難度：0.8
解析
2．下列各組數中，是勾股數的是（　　）
A．0.3，0.4，0.5 B．3，4，5
C．
3
，
4
，
5
D．5，7，12
組卷：116引用：3難度：0.7
解析
3．下列二次根式中，是最簡二次根式的是（　　）
A．
32
B．
90
C．
3
2
D．
5
組卷：130引用：6難度：0.7
解析
4．下列運算正確的是（　　）
A．
3
+
6
=
9
B．
3
5
-
5
=
2
C．
24
÷
6
=
4
D．
3
×
5
=
15
組卷：150引用：7難度：0.6
解析
5．下列說法中，錯誤的是（　　）
A．8的立方根是±2
B．4的算術平方根是2
C．
81
的平方根是±3
D．立方根等于-1的實數是-1
組卷：1828引用：13難度：0.7
解析
6．如圖，一支鉛筆放在圓柱體筆筒中，筆筒的內部底面直徑是9cm,內壁高12cm,則這支鉛筆的長度可能是（　　）
A．9cm B．12cm C．15cm D．18cm
組卷：1703引用：20難度：0.7
解析
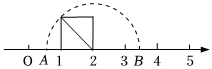7．如圖，以數軸的單位長度線段為邊作一個正方形，以表示數2的點為圓心，正方形對角線長為半徑畫半圓，交數軸于點A和點B，則點A表示的數是（　　）
?
A．
2
+
2
B．
2
-
2
C．
2
D．
1
-
2
組卷：1103引用：9難度：0.8
解析
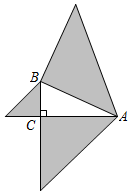8．如圖，以Rt△ABC的三邊為直角邊分別向外作等腰直角三角形．若
AB
=
3
，則圖中陰影部分的面積為（　　）
A．3 B．
9
2
C．
3
2
D．
3
5
組卷：1954引用：14難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共13小題，計81分.解答應寫出過程）

25．我們之前學習有理數時，知道兩個數的乘積為1則這兩個數互為倒數．在學習二次根式的過程中，小明研究發現有一些特殊的無理數之間具有互為倒數的關系．例如：由
（
2
+
1
）
（
2
-
1
）
=
1
，可得
2
+
1
與
2
-
1
互為倒數，即
1
2
+
1
=
2
-
1
或
1
2
-
1
=
2
+
1
，類似地，
（
3
+
2
）
（
3
-
2
）
=
1
，可得
1
3
+
2
=
3
-
2
或
1
3
-
2
=
3
+
2
．
根據小明發現的規律，解決下列問題：
（1）
1
7
+
6
=
，
1
n
+
1
+
n
=
（n為正整數）；
（2）若
1
2
3
+
a
=
2
3
-
a
，則a=
；
（3）求
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+
…
+
1
100
+
99
的值．
組卷：140引用：4難度：0.6
解析
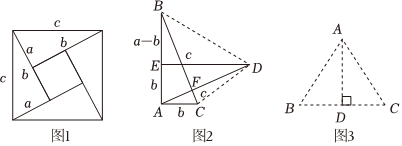26．【背景介紹】勾股定理是幾何學中的明珠，充滿著魅力．如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，用它可以證明勾股定理，思路是大正方形的面積有兩種求法，一種是等于c²另一種是等于四個直角三角形與一個小正方形的面積之和，即
1
2
ab
×
4
+
（
b
-
a
）
2
從而得到等式
c
2
=
1
2
ab
×
4
+
（
b
-
a
）
2
化簡使得結論a²+b²=c²這里用兩種求法來表示同一個量從而得到等式或方程的方法，我們稱之為“雙求法”．
【方法運用】千百年來，人們對勾股定理的證明趨之若鶩，其中有著名的數學家，也有業余數學愛好者．向常春在2010年構造發現了一個新的證法：把兩個全等的Rt△ABC和Rt△DEA如圖2放置，其三邊長分別為a,b,c,∠BAC=∠DEA=90°顯然BC⊥AD．
（1）請用a,b,c分別表示出四邊形ABDC，梯形AEDC，△EBD的面積，再探究這三個圖形面積之間的關系，證明勾股定理a²+b²=c²；
【方法遷移】
（2）如圖3，在△ABC中，AD是BC邊上的高，AB=4，AC=5，BC=6，設BD=x,求x的值．
組卷：504引用：2難度：0.5
解析