2022-2023學年山西省太原市小店區八年級（下）期末數學試卷
發布：2024/6/23 8:0:10
一、選擇題。（本大題共10個小題）在每小題給出的四個選項中，只有一個符合題目要求，請選出并在答題卡上將該項涂黑.
-
1．下列x的值中，使分式
無意義的是（ ）x-2x-3組卷：79引用：1難度：0.8 -
2．為了清晰準確地傳遞信息，更有效地引導旅客，機場標識系統設計必須做到規范化．下面是民用機場常用公共信息的標識，其中的圖案是中心對稱圖形的是（ ）
組卷：25引用：1難度：0.8 -
3．運用提公因式法將多項式“6ab2-12a3b2c”分解因式，應提取的公因式是（ ）
組卷：259引用：2難度：0.7 -
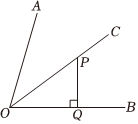4．如圖，OC平分∠AOB，點P在OC上，PQ⊥OB于點Q．若OP=5，OQ=4，則點P到OA的距離為（ ）
?組卷：146引用：1難度：0.5 -
5．若關于x的不等式ax＞b的解集是x＜
，則a的取值范圍是（ ）ba組卷：174引用：1難度：0.5 -
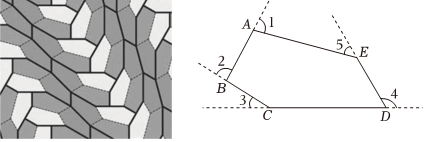6．完美五邊形是指可以無重疊、無間隙鋪滿整個平面的凸五邊形．如圖的五邊形ABCDE是迄今為止人類發現的第15種完美五邊形，其中∠1，∠2，∠3，∠4，∠5的度數和為（ ）組卷：333引用：3難度：0.8 -
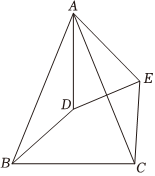7．如圖，△ABC，△ADE均是頂角為40°的等腰三角形，BC，DE分別是底邊．圖中的△ACE可由△ABD旋轉得到，其旋轉中心與旋轉角度數分別是（ ）
?組卷：91引用：1難度：0.7
三、解答題。（本大題共8個小題）解答應寫出必要的文字說明、證明過程或演算步驟。
-
22．閱讀以下材料，并按要求完成相應的任務：
任務：等腰梯形
在第六章，我們按照“定義一性質一判定”的路徑研究了平行四邊形．生活中還有另一種特殊四邊形一等腰梯形，我們可以類比平行四邊形對其進行研究．
定義：只有一組對邊平行的四邊形叫做梯形，其中互相平行的兩邊叫做底，不平行的兩邊叫做腰．兩腰相等的梯形叫做等腰梯形．
如圖1，四邊形ABCD是等腰梯形，其中AD∥BC，AB=DC．
性質：從整體對稱性看，等腰梯形是軸對稱圖形：
從局部元素特征看，等腰梯形有如下性質：
性質1：等腰梯形同一底上的兩個角相等；性質2：…?
判定：與平行四邊形類似，等腰梯形的性質與判定也具有互逆關系
判定1：…．?
（1）為證明等腰梯形的性質1，小穎的思考如下．請按她的思路選擇一種方法寫出證明過程．
已知：如圖2，四邊形ABCD是等腰梯形，AD∥BC，AB=DC．
求證：∠B=∠C，∠A=∠D．
證明：方法1：過點A作DC的平行線，交BC于點E，…；
方法2：過點A，D作BC的垂線，垂足分別為M，N，…．
（2）根據材料中的思路，小穎由等腰梯形的性質1得到關于等腰梯形判定方法的猜想，請你補全該命題，并判斷其真假：的梯形是等腰梯形，該命題是 命題．?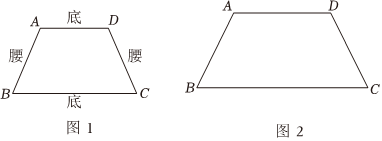
組卷：96引用：2難度：0.1 -
23．綜合與實踐
問題情境：活動課上，同學們以三角形為背景探究圖形變化中的數學問題．如圖1，△ABC中，∠ACB=90°，∠A=30°．將△ABC從圖1的位置開始繞點C順時針旋轉得到△A'B'C（點A，B的對應點分別為點A′，B'），旋轉角為α（0°＜α＜180°）．
操作思考：（1）如圖2，“明辨”小組畫出了A'B'恰好經過點B時的圖形．求此時旋轉角α的度數；
（2）如圖3，“善思”小組畫出了點A'落在CB延長線上時的圖形，此時點B'也恰好在AC的延長線上．過點B作AC的平行線交AA′于點P，連接BB'．猜想線段AP與BB'的數量關系，并說明理由；
拓展探究：（3）如圖4，“博學”小組在圖2的基礎上，將△BCB′沿射線A'C的方向平移，點B，C，B′的對應點分別為D，E，F．若AB=4，當以A，B'，D為頂點的三角形是等腰三角形時，請直接寫出平移的距離．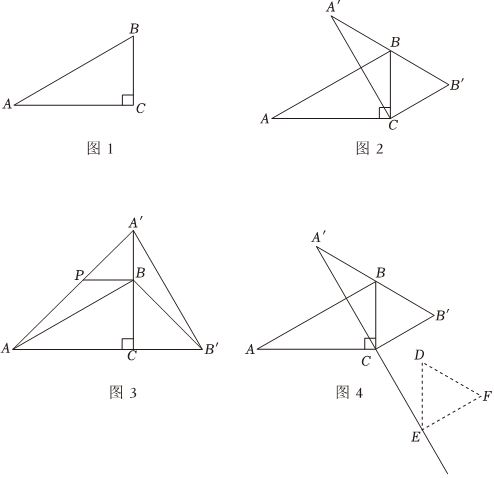
?組卷：622引用：3難度：0.1