當前位置：試卷中心 > 試卷詳情

2023年陜西省西安市新城區大明宮中學中考數學二模試卷

發布：2024/4/20 14:35:0

一、選擇題（本大題共8小題，每小題3分，滿分24分）

1．-2的倒數是（　　）
A．-2 B．2 C．-
1
2
D．
1
2
組卷：74引用：4難度：0.9
解析
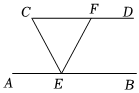2．如圖，AB∥CD，EC平分∠AEF，且∠AEC=65°，則∠EFD的大小為（　　）
A．100° B．120° C．130° D．140°
組卷：175引用：1難度：0.6
解析
3．計算（-2m²n³）²的結果是（　　）
A．-2m⁴n⁶ B．4m⁴n⁶ C．4m⁴n⁵ D．-4m⁴n⁵
組卷：329引用：4難度：0.7
解析
4．一次函數y=-2x+3的圖象向上移2個單位長度后，與y軸相交的點坐標為（　　）
A．（0，5） B．（0，1） C．（5，0） D．（1，0）
組卷：527引用：4難度：0.5
解析
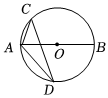5．如圖，AB為⊙O的直徑，C、D為⊙O上的兩點，若∠BAC=68°，則∠D的度數為（　　）
A．68° B．34° C．32° D．22°
組卷：286引用：3難度：0.6
解析
6．2022年世界杯足球賽舉世矚目，某大型企業為獎勵年度優秀員工，預定了小組賽和決賽兩個階段的門票共20張作為獎品，總價為74000元．已知小組賽門票每張2800元，決賽門票每張6400元，設該企業預定了小組賽門票x張，決賽門票y張，根據題意可列方程組為（　　）
A．
x
+
y
=
20
2800
x
+
6400
y
=
74000
B．
x
+
y
=
20
6400
x
+
2800
y
=
74000
C．
x
-
y
=
20
2800
x
+
6400
y
=
74000
D．
x
+
y
=
20
6400
y
=
74000
+
2800
x
組卷：491引用：6難度：0.6
解析
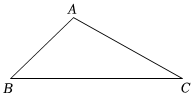7．如圖，在△ABC中，tanB=1，sinC=
1
2
，AB=
2
，則邊BC的長為（　　）
A．
2
3
-
1
B．
3
+
1
C．
2
+
1
D．
2
2
-
1
組卷：216引用：1難度：0.8
解析
8．已知二次函數y=ax²+bx+c,其中y與x的部分對應值如表．則下列結論中正確的是（　　）

x … 0 1 2 3 4 5 …

y … -3 -4 -3 0 5 12 …

A．abc＜0
B．
b
2
a
=
1
C．4a+2b+c＞0
D．方程ax²+bx+c=0的兩個根分別是x₁=-1，x₂=3
組卷：152引用：1難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共13小題，滿分81分.解答應寫出過程）

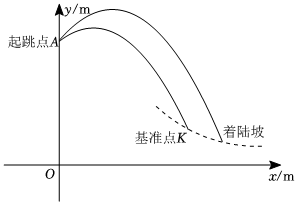25．跳臺滑雪運動可分為助滑、起跳、飛行和落地四個階段，運動員起跳后飛行的路線是拋物線的一部分（如圖中實線部分所示），落地點在著陸坡（如圖中虛線部分所示）上，著陸坡上的基準點K為飛行距離計分的參照點，落地點超過K點越遠，飛行距離分越高．某滑雪賽場跳臺滑雪的起跳臺的高度OA為60m,基準點K到起跳臺的水平距離為70m,高度為18m.設運動員從起跳點A起跳后的高度y（m）與水平距離x（m）之間的函數關系為
y
=
-
1
50
x
2
+
bx
+
c
．
（1）若運動員落地點恰好到達K點，求b,c的值．
（2）若運動員飛行的水平距離為21m,恰好達到最大高度68.82m,試判斷他的落地點能否超過K點，并說明理由．
組卷：290引用：3難度：0.5
解析
26．問題提出：
（1）如圖①，在Rt△ABC中，∠B=90°，AB=5，BC=12．若P是邊AC上一點，則BP的最小值為
．
問題探究：
（2）如圖②，在Rt△ABC中，AB=BC，斜邊AC的長為
4
2
，E是BC的中點，P是邊AC上一點，試求PB+PE的最小值．
問題解決：
（3）某城區有一個五邊形MBCDP空地（∠M=∠P=∠PDC=90°，∠C=150°），城建部門計劃利用該空地建造一個居民戶外活動廣場，其中△MAB的部分規劃為觀賞區，用于種植各類鮮花，△APD部分規劃為音樂區，供老年合唱團排練合唱或廣場舞使用，四邊形ABCD部分為市民健身廣場，如圖③所示．已知AD=100米，CD=50米，∠BAD=60°，∠ABC=90°．為了進一步提升服務休閑功能，滿足市民游園和健身需求，現要在AB，AD上分別取點E，F，鋪設一條由CE，EF，FC連接而成的步行景觀道，已知鋪設景觀道的成本為100元/米，求鋪設完這條步行景觀道所需的最低成本．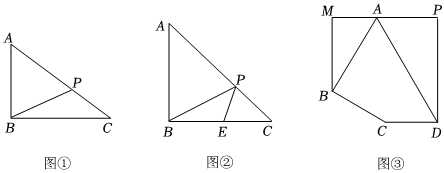
組卷：771引用：5難度：0.2
解析