2023年上海市閔行區(qū)高考數(shù)學(xué)二模試卷

一、填空題（本大題共有12題，滿分54分，第1～6題每題4分，第7～12題每題5分）考生應(yīng)在答題紙的相應(yīng)位置直接填寫結(jié)果．

• 1．設(shè)全集U={-2，-1，0，1，2}，集合A={-2，0，2}，則

  A

  =

  ．
  組卷：116引用：2難度：0.9

  解析

• 2．若實數(shù)x、y滿足lgx=m、y=10^1-m，則xy=

  ．
  組卷：206引用：2難度：0.7

  解析

• 3．已知復(fù)數(shù)z滿足z（1-i）=i（i為虛數(shù)單位），則z的虛部為

  ．
  組卷：124引用：3難度：0.8

  解析

• 4．已知圓柱的底面積為9π，側(cè)面積為12π，則該圓柱的體積為

  ．
  組卷：196引用：3難度：0.8

  解析

• 5．已知常數(shù)m＞0，

  （

  x

  +

  m

  x

  ）

  6

  的二項展開式中x²項的系數(shù)是60，則m的值為

  ．
  組卷：137引用：3難度：0.9

  解析

• 6．已知事件A與事件B互斥，如果P（A）=0.3，P（B）=0.5，那么

  P

  （

  A

  ∪

  B

  ）

  =

  ．
  組卷：250引用：6難度：0.8

  解析

• 7．今年春季流感爆發(fā)期間，某醫(yī)院準(zhǔn)備將2名醫(yī)生和4名護(hù)士分配到兩所學(xué)校，給學(xué)校老師和學(xué)生接種流感疫苗．若每所學(xué)校分配1名醫(yī)生和2名護(hù)士，則不同的分配方法數(shù)為

  ．
  組卷：262引用：7難度：0.8

  解析

三、解答題（本大題滿分78分）本大題共有5題，解答下列各題必須在答題紙相應(yīng)編

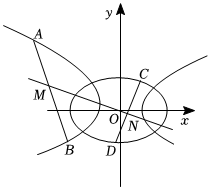• 20．已知O為坐標(biāo)原點(diǎn)，曲線C₁：

  x

  2

  a

  2

  -

  y

  2

  =1（a＞0）和曲線C₂：

  x

  2

  4

  +

  y

  2

  2

  =1有公共點(diǎn)，直線l₁：y=k₁x+b₁與曲線C₁的左支相交于A、B兩點(diǎn)，線段AB的中點(diǎn)為M．
  （1）若曲線C₁和C₂有且僅有兩個公共點(diǎn)，求曲線C₁的離心率和漸近線方程；
  （2）若直線OM經(jīng)過曲線C₂上的點(diǎn)

  T

  （

  2

  ，-

  1

  ）

  ，且a²為正整數(shù)，求a的值；
  （3）若直線l₂：y=k₂x+b₂與曲線C₂相交于C、D兩點(diǎn)，且直線OM經(jīng)過線段CD中點(diǎn)N，求證：

  k

  2

  1

  +

  k

  2

  2

  ＞1．
  組卷：251引用：1難度：0.5

  解析

• 21．如果曲線y=f（x）存在相互垂直的兩條切線，稱函數(shù)y=f（x）是“正交函數(shù)”．已知f（x）=x²+ax+2lnx,設(shè)曲線y=f（x）在點(diǎn)M（x₀，f（x₀））處的切線為l₁．
  （1）當(dāng)f'（1）=0時，求實數(shù)a的值；
  （2）當(dāng)a=-8，x₀=8時，是否存在直線l₂滿足l₁⊥l₂，且l₂與曲線y=f（x）相切？請說明理由；
  （3）當(dāng)a≥-5時，如果函數(shù)y=f（x）是“正交函數(shù)”，求滿足要求的實數(shù)a的集合D；若對任意a∈D，曲線y=f（x）都不存在與l₁垂直的切線l₂，求x₀的取值范圍．
  組卷：331引用：4難度：0.3

  解析