2022-2023學(xué)年湖南師大附中高三（上）月考數(shù)學(xué)試卷（六）

一、選擇題。本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．已知復(fù)數(shù)z滿足

  z

  1

  -

  i

  -

  i

  1

  +

  i

  =

  1

  ，則z=（　　）

  A．-2+i

  B．-2-i

  C．2+i

  D．2-i
  組卷：65引用：5難度：0.8

  解析

• 2．已知集合A={（x,y）|x²+y²≤2，x∈Z，y∈Z}，B={（x,y）|x+1＞0}，則A∩B的元素個(gè)數(shù)為（　　）

  A．9

  B．8

  C．6

  D．5
  組卷：131引用：6難度：0.8

  解析

• 3．已知函數(shù)f（x）=3x-ln|x|，則f（x）的圖象大致為（　　）

  A．

  B．

  C．

  D．
  組卷：297引用：11難度：0.7

  解析

• 4．我國(guó)古代人民早在幾千年以前就已經(jīng)發(fā)現(xiàn)并應(yīng)用勾股定理了，勾股定理最早的證明是東漢數(shù)學(xué)家趙爽在為《周髀算經(jīng)》作注時(shí)給出的，被后人稱為“趙爽弦圖”．“趙爽弦圖”是數(shù)形結(jié)合思想的體現(xiàn)，是中國(guó)古代數(shù)學(xué)的圖騰，還被用作第24屆國(guó)際數(shù)學(xué)家大會(huì)的會(huì)徽．如圖，大正方形ABCD是由4個(gè)全等的直角三角形和中間的小正方形組成的，若

  AB

  =

  a

  ，

  AD

  =

  b

  ，E為BF的中點(diǎn)，則

  AE

  =（　　）

  A． 4 5 a + 2 5 b

  B． 2 5 a + 4 5 b

  C． 4 3 a + 2 3 b

  D． 2 3 a + 4 3 b
  組卷：1094引用：21難度：0.6

  解析

• 5．（a-x）（2+x）⁶的展開(kāi)式中x⁵的系數(shù)是12，則實(shí)數(shù)a的值為（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：420引用：6難度：0.6

  解析

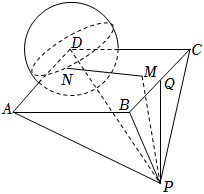• 6．如圖，四棱錐P-ABCD的底面是邊長(zhǎng)為2的正方形，Q為BC的中點(diǎn)，PQ⊥平面ABCD，且PQ=2，動(dòng)點(diǎn)N在以D為球心，半徑為1的球面上運(yùn)動(dòng)，點(diǎn)M在平面ABCD內(nèi)運(yùn)動(dòng)，且PM=

  5

  ，則MN長(zhǎng)度的最小值為（　　）

  A． 5 - 3 2

  B．2- 3

  C．-2+ 5

  D． 3 - 3 2
  組卷：112引用：4難度：0.5

  解析

• 7．設(shè)

  a

  =

  1

  4

  ，

  b

  =

  e

  sin

  1

  8

  -

  1

  ，

  c

  =

  ln

  9

  7

  ，e為自然對(duì)數(shù)的底數(shù)，則（　　）

  A．a(chǎn)＞b＞c

  B．a(chǎn)＞c＞b

  C．c＞a＞b

  D．b＞c＞a
  組卷：36引用：1難度：0.5

  解析

四、解答題。本題共6小題，共70分．解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．過(guò)拋物線y²=2px（p＞0）的對(duì)稱軸上的定點(diǎn)M（m,0）（m＞0），作直線AB與拋物線相交于A，B兩點(diǎn)．
  （1）試證明A，B兩點(diǎn)的縱坐標(biāo)之積為定值；
  （2）若點(diǎn)N是定直線l：x=-m上的任意一點(diǎn)，分別記直線AN，MN，BN的斜率為k₁、k₂、k₃，
  試求k₁、k₂、k₃之間的關(guān)系，并給出證明．
  組卷：368引用：6難度：0.1

  解析

• 22．已知函數(shù)f（x）=e^xsinx-cosx,g（x）=xcosx-

  2

  e^x，其中e是自然對(duì)數(shù)的底數(shù)．
  （1）判斷函數(shù)y=f（x）在（0，

  π

  2

  ）內(nèi)的零點(diǎn)的個(gè)數(shù)，并說(shuō)明理由；
  （2）?x₁∈[0，

  π

  2

  ]，?x₂∈[0，

  π

  2

  ]，使得f（x₁）+g（x₂）≥m成立，試求實(shí)數(shù)m的取值范圍；
  （3）若x＞-1，求證：f（x）-g（x）＞0．
  組卷：881引用：15難度：0.1

  解析