人教新版八年級上冊《第14章 整式的乘法與因式分解》2023年單元測試卷（9）

一、選擇題

• 1．下列計算中正確的是（　　）

  A．a3?a2=a6	B．（a2b）3=a6b
  C．a3+a2=a5	D．（-x）5?（-x）3=x8
  組卷：114引用：2難度：0.9

  解析

• 2．計算（x-1）（x²+x+1）的結果應是（　　）

  A．x3-1	B．x3+1
  C．x3-2x-1	D．x3-2x2+2x-1
  組卷：138引用：2難度：0.7

  解析

• 3．下列各多項式中不能用公式法分解的是（　　）

  A．x2-（-y）2

  B．a2-ab+ 1 4 b2

  C．x2-2x-1

  D．25-10x+x2
  組卷：69引用：2難度：0.7

  解析

• 4．若x^m÷x²ⁿ⁺¹=x,則m與n的關系是（　　）

  A．m=2n+1

  B．m=-2n-1

  C．m-2n=2

  D．m-2n=-2
  組卷：1647引用：8難度：0.9

  解析

• 5．若2^m=5，4ⁿ=3，則4^3n-m的值是（　　）

  A． 9 10

  B． 27 25

  C．2

  D．4
  組卷：2158引用：8難度：0.7

  解析

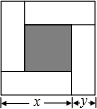• 6．如圖，大正方形的邊長為m,小正方形的邊長為n,若用x、y表示四個相同長方形的兩邊長（x＞y），給出以下關系式：①x+y=m；②x-y=n；③xy=

  m

  2

  -

  n

  2

  4

  ．其中正確的關系式的個數有（　　）

  A．0個

  B．1個

  C．2個

  D．3個
  組卷：1306引用：3難度：0.7

  解析

• 7．下列各式中，計算正確的是（　　）

  A．（-5an+1b）?（-2a）=10an+1b

  B．（-4a2b）?（-a2b2）? 1 2 b 3 c = 2 a 4 b 6 c

  C．（-3xy）?（-x2z）?6xy2=3x3y3z

  D． （ 2 a n b 3 ） （ - 1 6 a b n - 1 ） = 1 3 a n + 1 b 3 n - 1
  組卷：1525引用：4難度：0.7

  解析

• 8．觀察下列等式：9-1=8，16-4=12，25-9=16，36-16=20，…設n表示正整數，下面符合上述規律的等式是（　　）

  A．（n+2）2-n2=4（n+1）	B．（n+1）2-（n-1）2=4n
  C．（n+2）2-n2=4n+1	D．（n+2）2-n2=2（n+1）
  組卷：211引用：7難度：0.9

  解析

• 9．已知（m-n）²=32，（m+n）²=4000，則m²+n²的值為（　　）

  A．2014

  B．2015

  C．2016

  D．4032
  組卷：1052引用：8難度：0.7

  解析

三、解答題

• 27．閱讀理解并填空：
  （1）為了求代數式x²+2x+3的值，我們必須知道x的值．
  若x=1，則這個代數式的值為

  ，
  若x=2，則這個代數式的值為

  ，
  …可見，這個代數式的值因x的取值不同而變化，盡管如此，我們還是有辦法來考慮這個代數式的值的范圍．
  （2）把一個多項式進行部分因式分解可以解決求代數式的最大（或最小）值問題．
  例如x²+2x+3=x²+2x+1+2=（x+1）²+2，因為（x+1）²是非負數，所以這個代數式的最小值是

  ，此時相應的x的值是

  ．
  （3）求代數式x²-12x+35的最小值，并寫出相應的x的值．
  （4）求代數式-x²-6x+12的最大值，并寫出相應的x的值．
  組卷：901引用：3難度：0.3

  解析

• 28．已知a,b,c是△ABC的三邊，試判斷（a²+b²+c²）²與4a²b²的大小．
  組卷：53引用：2難度：0.7

  解析