2022年重慶市高考數學調研試卷（三）

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設i為虛數單位，復數

  z

  =

  4

  +

  3

  i

  3

  -

  4

  i

  在復平面內所對應的點位于（　　）

  A．第一象限

  B．第四象限

  C．實軸上

  D．虛軸上
  組卷：143引用：1難度：0.8

  解析

• 2．已知集合A={-1，0，1}，B={a+b|a∈A，b∈A}，則集合A∪B中元素個數為（　　）

  A．3個

  B．4個

  C．5個

  D．6個
  組卷：175引用：1難度：0.7

  解析

• 3．設a∈R，則“a＞3”是“

  3

  a

  ＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：192引用：2難度：0.7

  解析

• 4．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F₂，點A在y軸上，△AF₁F₂為等邊三角形，且線段AF₂的中點恰在雙曲線C上，則雙曲線C的離心率為（　　）

  A． 3

  B．2

  C． 3 + 1

  D． 2 3 + 1
  組卷：181引用：1難度：0.6

  解析

• 5．已知等比數列{a_n}的前n項和為S_n，且a₂，3a₅，9a₈成等差數列，則

  S

  6

  S

  3

  =（　　）

  A． 1 3

  B． 4 3

  C．3

  D．4
  組卷：503引用：9難度：0.7

  解析

• 6．已知曲線C：

  y

  =

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

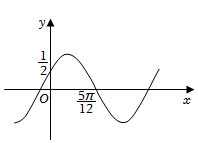  的部分圖象如圖所示，要得到曲線C的圖象，可將曲線y=cosx的圖象（　　）

  A．先向右平移 π 3 個單位長度，再將各點的橫坐標縮短到原來的 1 2 倍，縱坐標不變

  B．先向右平移 π 3 個單位長度，再將各點的橫坐標伸長到原來的2倍，縱坐標不變

  C．先向左平移 π 6 個單位長度，再將各點的橫坐標縮短到原來的 1 2 倍，縱坐標不變

  D．先向左平移 π 6 個單位長度，再將各點的橫坐標伸長到原來的2倍，縱坐標不變
  組卷：200引用：1難度：0.7

  解析

• 7．設函數f（x）=

  - 2 x + 2 - x （ x ＞ 0 ）

  - x 3 （ x ≤ 0 ）

  ，若a=ln2，b=3^0.2，c=log_0.32，則（　　）

  A．f（a）＞f（b）＞f（c）	B．f（b）＞f（a）＞f（c）
  C．f（a）＞f（c）＞f（b）	D．f（c）＞f（a）＞f（b）
  組卷：107引用：4難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．為有效防控新冠疫情從境外輸入，中國民航局根據相關法律宣布從2020年6月8日起實施航班熔斷機制，即航空公司同一航線航班，入境后核酸檢測結果為陽性的旅客人數達到一定數量的民航局對其發出“熔斷”指
  令，暫停該公司該航線的運行（達到5個暫停運行1周，達到10個暫停運行4周），并規定“熔斷期”的航班量
  不得調整用于其他航線，“熔斷期”結束后，航空公司方可恢復每周1班航班計劃．已知某國際航空公司A航線
  計劃每周有一次航班入境，該航線第一次航班被熔斷的概率是

  1

  2

  ，且被熔斷的一次航班的下一次航班也被熔斷的概率是

  1

  2

  ，未被熔斷的一次航班的下一次航班也未被熔斷的概率是

  2

  3

  ．一條航線處于“熔斷期”的原計劃航
  班不記入該航線的航班次數，記該航空公司A航線的第n次航班被熔斷的概率為p_n．
  （1）求p₂；
  （2）證明：

  {

  p

  n

  -

  2

  5

  }

  為等比數列；
  （3）求數列{p_n}的前n項和T_n，并說明T_n的實際意義．
  組卷：292引用：3難度：0.5

  解析

• 22．已知函數f（x）=xe^2x-（1+lnx）．
  （1）證明：f（x）≥2x；
  （2）對?x₁∈（0，+∞），x₂∈（0，e]，不等式

  x

  1

  x

  2

  （

  e

  2

  x

  1

  +

  aln

  x

  2

  ）

  ≥

  a

  x

  1

  +

  x

  2

  （

  ln

  x

  1

  +

  1

  ）恒成立，求實數a的取值范圍．
  組卷：139引用：1難度：0.3

  解析