2022-2023學年浙江省寧波市余姚市蘭江中學八年級（上）期中數(shù)學試卷

一.選擇題（共10小題，滿分30分，每小題3分）

• 1．三角形是指（　　）

  A．由三條線段所組成的封閉圖形

  B．由不在同一直線上的三條直線首尾順次相接組成的圖形

  C．由不在同一直線上的三條線段首尾順次相接組成的圖形

  D．由三條線段首尾順次相接組成的圖形
  組卷：1458引用：7難度：0.7

  解析

• 2．下列數(shù)值是不等式x＜2的解的是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：294引用：5難度：0.8

  解析

• 3．下列各組長度的三條線段能組成三角形的是（　　）

  A．1，2，3

  B．1，1，2

  C．2，2，3

  D．1，3，7
  組卷：276引用：8難度：0.7

  解析

• 4．下列對△ABC的判斷，錯誤的是（　　）

  A．若∠A：∠B：∠C=1：2：3，則△ABC是直角三角形

  B．若∠A=30°，∠B=50°，則△ABC是銳角三角形

  C．若AB=AC，∠B=40°，則△ABC是鈍角三角形

  D．若2∠A=2∠B=∠C，則△ABC是等腰直角三角形
  組卷：2278引用：14難度：0.6

  解析

• 5．下列生活實例中，利用了“三角形穩(wěn)定性”的是（　　）

  A．

  B．

  C．

  D．
  組卷：997引用：13難度：0.7

  解析

• 6．若等腰三角形的兩邊長分別為2和5，則它的周長為（　　）

  A．9

  B．7

  C．12

  D．9或12
  組卷：5075引用：49難度：0.9

  解析

• 7．如果將一副三角板按如圖的方式疊放，則∠1的度數(shù)為（　　）

  A．105°

  B．120°

  C．75°

  D．45°
  組卷：1663引用：16難度：0.7

  解析

• 8．定義新運算“⊕”如下：當a＞b時，a⊕b=ab+b；當a＜b時，a⊕b=ab-b,若3⊕（x+2）＞0，則x的取值范圍是（　　）

  A．-1＜x＜1或x＜-2	B．x＜-2或1＜x＜2
  C．-2＜x＜1或x＞1	D．x＜-2或x＞2
  組卷：1304引用：10難度：0.6

  解析

三.解答題（共8小題，滿分66分）

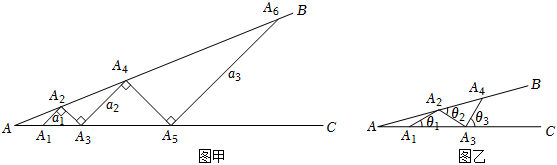
• 23．某數(shù)學興趣小組開展了一次活動，過程如下：設∠BAC=θ（0°＜θ＜90°）．現(xiàn)把小棒依次擺放在兩射線之間，并使小棒兩端分別落在射線AB、AC上．
  
  活動一：
  如圖甲所示，從點A₁開始，依次向右擺放小棒，使小棒與小棒在端點處互相垂直，A₁A₂為第1根小棒．
  數(shù)學思考：（1）小棒能無限擺下去嗎？答：

  ．（填“能”或“不能”）
  （2）設AA₁=A₁A₂=A₂A₃，θ=

  ；
  活動二：
  如圖乙所示，從點A₁開始，用等長的小棒依次向右擺放，其中A₁A₂為第1根小棒，且A₁A₂=AA₁．
  數(shù)學思考：（3）若已經(jīng)擺放了3根小棒，θ₃=

  ；（用含θ的式子表示）
  （4）若只能擺放5根小棒，求θ的范圍．
  組卷：1036引用：6難度：0.6

  解析

• 24．【發(fā)現(xiàn)問題】小強在一次學習過程中遇到了下面的問題：如圖①，AD是△ABC的中線，若AB=5，AC=3，求AD的取值范圍．
  
  【探究方法】小強所在的小組通過探究發(fā)現(xiàn)，延長AD至點E．使ED=AD．連接BE．
  可以證出△ADC≌△EDB，利用全等三角形的性質(zhì)可將已知的邊長與AD轉化到△ABE中，進而求出AD的取值范圍．
  方法小結：從上面的思路可以看出，解決問題的關鍵是將中線AD延長一倍，構造出全等三角形，我們把這種方法叫做“倍長中線法”．
  （1）請你利用上面解答問題的思路方法，寫出求AD的取值范圍的過程；
  【問題解決】
  （2）如圖②，CB是△AEC的中線，CD是△ABC的中線，且AB=AC，下列四個選項中：
  A．∠ACD=∠BCD
  B．CE=2CD
  C．∠BCD=∠BCE
  D．CD=CB
  直接寫出所有正確選項的序號是

  ．
  【問題拓展】
  （3）如圖③，在△ABO和△CDO中，OA=OB，OC=OD，∠AOB與∠COD互補，連接AC、BD，E是BD的中點，求證：OE=

  1

  2

  AC．
  組卷：486引用：2難度：0.3

  解析