滬科版八年級下冊《第十八章 勾股定理》2018年單元測試卷（湖南省長沙市開福區湘一實驗中學）

一、選擇題（每小題3分，共30分，每小題只有一個選項符合題意）

• 1．如圖，等邊△OAB的邊長為2，則點B的坐標為（　　）

  A．（1，1）

  B．（ 3 ，1）

  C．（ 3 ， 3 ）

  D．（1， 3 ）
  組卷：814引用：9難度：0.7

  解析

• 2．如圖，小巷左右兩側是豎直的墻，一架梯子斜靠在左墻時，梯子底端到左墻角的距離為0.7米，頂端距離地面2.4米．如果保持梯子底端位置不動，將梯子斜靠在右墻時，頂端距離地面2米，則小巷的寬度為（　　）

  A．0.7米

  B．1.5米

  C．2.2米

  D．2.4米
  組卷：9870引用：59難度：0.7

  解析

• 3．《九章算術》中的“折竹抵地”問題：今有竹高一丈，末折抵地，去根六尺．問折高者幾何？意思是：一根竹子，原高一丈（一丈=10尺），一陣風將竹子折斷，其竹梢恰好抵地，抵地處離竹子底部6尺遠，問折斷處離地面的高度是多少？設折斷處離地面的高度為x尺，則可列方程為（　　）

  A．x2-6=（10-x）2	B．x2-62=（10-x）2
  C．x2+6=（10-x）2	D．x2+62=（10-x）2
  組卷：5365引用：63難度：0.7

  解析

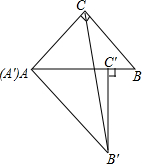• 4．如圖，將兩個大小、形狀完全相同的△ABC和△A′B′C′拼在一起，其中點A′與點A重合，點C′落在邊AB上，連接B′C．若∠ACB=∠AC′B′=90°，AC=BC=3，則B′C的長為（　　）

  A．3 3

  B．6

  C．3 2

  D． 21
  組卷：6993引用：23難度：0.7

  解析

• 5．下列說法中正確的是（　　）

  A．已知a,b,c是三角形的三邊長，則a2+b2=c2

  B．在直角三角形中，兩邊長和的平方等于第三邊長的平方

  C．在Rt△ABC中，若∠C=90°，則三角形對應的三邊滿足a2+b2=c2

  D．在Rt△ABC中，若∠A=90°，則三角形對應的三邊滿足a2+b2=c2
  組卷：384引用：2難度：0.9

  解析

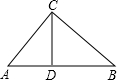
• 6．如圖，在△ABC中，已知∠ACB=90°，BC=6，AC=8，點D在AB上，且BD=BC，則AD的長是（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：255引用：1難度：0.7

  解析

• 7．如圖，在Rt△ABC中，∠ACB=90°，AB=

  13

  ，BC=2，則這個直角三角形的面積為（　　）

  A．3

  B．6

  C． 13

  D． 1 2 13
  組卷：188引用：4難度：0.7

  解析

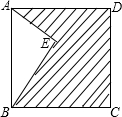• 8．如圖，點E在正方形ABCD內，滿足∠AEB=90°，AE=6，BE=8，則陰影部分的面積是（　　）

  A．48

  B．60

  C．76

  D．80
  組卷：3526引用：139難度：0.9

  解析

六、（本題滿分8分）

• 25．（1）如圖（1），分別以Rt△ABC三邊為直徑向外作三個正方形，其面積分別用S₁，S₂，S₃表示，寫出S₁，S₂，S₃之間關系．（不必證明）
  （2）如圖（2），分別以Rt△ABC三邊為邊向外作三個半圓，其面積分別用S₁，S₂，S₃表示，確定它們的關系證明；
  （3）如圖（3），分別以Rt△ABC三邊為邊向外作正三角形，其面積分別用S₁，S₂，S₃表示，確定它們的關系并證明．
  
  組卷：4062引用：5難度：0.1

  解析

七、（本題滿分8分）

• 26．勾股定理神秘而美妙，它的證法多樣，其巧妙各有不同，其中的“面積法”給了小聰以靈感，他驚喜的發現，當兩個全等的直角三角形如圖1或圖2擺放時，都可以用“面積法”來證明，下面是小聰利用圖1證明勾股定理的過程：
  將兩個全等的直角三角形按圖1所示擺放，其中∠DAB=90°，求證：a²+b²=c²
  證明：連接DB，過點D作BC邊上的高DF，則DF=EC=b-a
  ∵S_{四邊形ADCB}=S_△ACD+S_△ABC=

  1

  2

  b²+

  1

  2

  ab.
  又∵S_{四邊形ADCB}=S_△ADB+S_△DCB=

  1

  2

  c²+

  1

  2

  a（b-a）
  ∴

  1

  2

  b²+

  1

  2

  ab=

  1

  2

  c²+

  1

  2

  a（b-a）
  ∴a²+b²=c²
  請參照上述證法，利用圖2完成下面的證明．
  將兩個全等的直角三角形按圖2所示擺放，其中∠DAB=90°．求證：a²+b²=c²．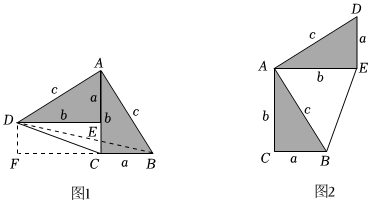
  
  組卷：4160引用：24難度：0.3

  解析