2023年湖北省襄陽五中高考數(shù)學適應性試卷（一）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設復數(shù)X，則在復平面內

  z

  +

  1

  z

  對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：26引用：2難度：0.8

  解析

• 2．函數(shù)

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  e

  x

  +

  1

  ?

  cosx

  的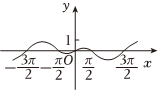圖象大致為（　　）

  A．	B．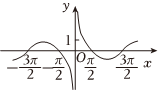
  C．	D．
  組卷：103引用：3難度：0.8

  解析

• 3．已知

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，

  sin

  4

  α

  1

  +

  cos

  4

  α

  =

  sinα

  cosα

  -

  2

  ，則

  tan

  α

  2

  =（　　）

  A． 15 5

  B． 5 3

  C． 15 15

  D． 5 5
  組卷：412引用：5難度：0.7

  解析

• 4．希伯特在1990年提出了孿生素數(shù)猜想：在自然數(shù)集中，孿生素數(shù)對有無窮多個，其中孿生素數(shù)是指相差2的素數(shù)對，即若p和p+2均是素數(shù)，素數(shù)對（p,p+2）稱為孿生素數(shù)，從16以內的素數(shù)中任意取兩個，其中能構成孿生素數(shù)的概率為（　　）

  A． 1 3

  B． 1 5

  C． 1 7

  D． 3 28
  組卷：66引用：3難度：0.6

  解析

• 5．希臘著名數(shù)學家阿波羅尼斯與歐幾里得、阿基米德齊名．他發(fā)現(xiàn)：“平面內到兩個定點A，B的距離之比為定值λ（λ≠1）的點的軌跡是圓”．后來，人們將這個圓以他的名字命名，稱為阿波羅尼斯圓，簡稱阿氏圓．已知在平面直角坐標系xOy中，A（-4，1），B（-4，4），若點P是滿足

  λ

  =

  1

  2

  的阿氏圓上的任意一點，點Q為拋物線C：y²=16x上的動點，Q在直線x=-4上的射影為R，則|PB|+2|PQ|+2|QR|的最小值為（　　）

  A． 4 5

  B． 8 5

  C． 65 2

  D． 2 65
  組卷：221引用：3難度：0.5

  解析

• 6．圖1中，正方體ABCD-EFGH的每條棱與正八面體MPORSN（八個面均為正三角形）的一條棱垂直且互相平分．將該正方體的頂點與正八面體的頂點連結，得到圖2的十二面體，該十二面體能獨立密鋪三維空間．若AB=1，則點M到直線RG的距離等于（　　）
  

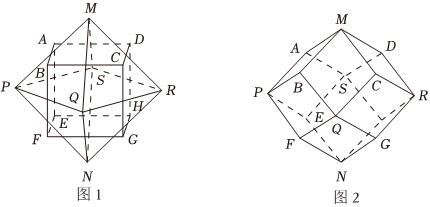
  A． 2

  B． 3

  C． 6 2

  D． 7 2
  組卷：83引用：4難度：0.6

  解析

• 7．在△ABC中，已知

  AD

  =

  2

  DC

  ，AC=3BC，sin∠BDC=3sin∠BAC，當

  CA

  ?

  CB

  -

  |

  AB

  |

  取得最小值時，△ABC的面積為（　　）

  A． 3 4

  B． 5 2

  C． 3 8

  D． 3 5 16
  組卷：466引用：3難度：0.5

  解析

四、解答題：（本大題共6小題，共70分，解答應寫出文字說明，證明過程或演算步驟）

• 21．已知離心率為

  2

  2

  的橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左焦點為F，左、右頂點分別為A₁、A₂，上頂點為B，且△A₁BF的外接圓半徑大小為

  3

  ．
  （1）求橢圓C方程；
  （2）設斜率存在的直線l交橢圓C于P，Q兩點（P，Q位于x軸的兩側），記直線A₁P、A₂P、A₂Q、A₁Q的斜率分別為k₁、k₂、k₃、k₄，若

  k

  1

  +

  k

  4

  =

  5

  3

  （

  k

  2

  +

  k

  3

  ）

  ，求△A₂PQ面積的取值范圍．
  組卷：187引用：6難度：0.5

  解析

• 22．如果曲線y=f（x）存在相互垂直的兩條切線，稱函數(shù)y=f（x）是“正交函數(shù)”．已知f（x）=x²+ax+2lnx,設曲線y=f（x）在點M（x₀，f（x₀））處的切線為l₁．
  （1）當f'（1）=0時，求實數(shù)a的值；
  （2）當a=-8，x₀=8時，是否存在直線l₂滿足l₁⊥l₂，且l₂與曲線y=f（x）相切？請說明理由；
  （3）當a≥-5時，如果函數(shù)y=f（x）是“正交函數(shù)”，求滿足要求的實數(shù)a的集合D；若對任意a∈D，曲線y=f（x）都不存在與l₁垂直的切線l₂，求x₀的取值范圍．
  組卷：331引用：4難度：0.3

  解析