2022-2023學年廣東省廣州市荔灣區高一（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．復數z滿足（1+2i）z=4+3i,則復數z=（　　）

  A．-2+i

  B．-2-i

  C．2+i

  D．2-i
  組卷：102引用：6難度：0.9

  解析

• 2．已知向量

  a

  =

  （

  2

  ，

  0

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，若

  a

  +

  λ

  b

  與

  b

  垂直，則λ等于（　　）

  A．1

  B．0

  C．-1

  D．-2
  組卷：165引用：2難度：0.7

  解析

• 3．一個小商店從一家食品有限公司購進10袋白糖，每袋白糖的標準質量是500g,為了了解這些白糖的質量情況，稱出各袋白糖的質量（單位：g）如下：495，500，503，508，498，500，493，500，503，500，記10袋白糖的平均質量為

  x

  ，標準差為s,則質量位于

  x

  -

  s

  與

  x

  +

  s

  之間的白糖袋數是（　　）

  A．6

  B．7

  C．8

  D．9
  組卷：123引用：2難度：0.8

  解析

• 4．已知事件A，B，且P（A）=0.7，P（B）=0.2，則（　　）

  A．若B?A，則P（A∪B）=0.7，P（AB）=0.14

  B．若A，B互斥，則P（A∪B）=0.9，P（AB）=0.14

  C．若A與B相互獨立，則P（A∪B）=0.9，P（AB）=0

  D．若A與B相互獨立，則 P （ A B ） = 0 . 24 ， P （ A B ） = 0 . 06
  組卷：278引用：2難度：0.7

  解析

• 5．已知

  a

  ，

  b

  ，

  c

  是同一平面內的三個向量，則（　　）

  A．若 a ∥ b ， b ∥ c ，則 a ∥ c

  B．若 a 是非零向量， b ≠ c ，則 a ? b = a ? c 是 a ⊥ （ b - c ） 的充要條件

  C．若 a = （ 1 ，- 1 ） ， b = （ 2 ，- 3 ） ， c = （ - 3 ， 4 ） ，則 { a + b ， c } 可以作為基底

  D．若 a ， b ， c 兩兩的夾角相等，且 | a | = 1 ， | b | = 1 ， | c | = 3 ，則 | a + b + c | = 2
  組卷：175引用：3難度：0.7

  解析

• 6．某小區從2000戶居民中隨機抽取100戶進行月用電量調查，發現他們的用電量都在50～350kW?h之間，進行適當的分組后（每組為左閉右開的區間），畫出頻率分布直方圖如圖所示．則（　　）
  

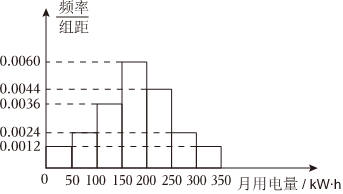
  A．小區用電量平均數為186.5，極差為300

  B．小區用電量中位數為171，眾數為175

  C．可以估計小區居民月用電量的85%分位數約為262.5

  D．小區用電量不小于250kW?h的約有380戶
  組卷：251引用：3難度：0.6

  解析

• 7．已知母線長為a的圓錐的側面展開圖為半圓，在該圓錐內放置一個圓柱，則當圓柱的側面積最大時，圓柱的體積為（　　）

  A． 3 128 π a 3

  B． 3 64 π a 3

  C． 3 32 π a 3

  D． 3 16 π a 3
  組卷：200引用：6難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

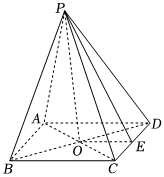• 21．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為2的正方形，AC與BD相交于點O，E為CD的中點，PA=PB=

  2

  ，∠PAD=∠PBC，
  （1）證明：平面POE⊥平面ABCD；
  （2）當點A到平面PCD的距離最大時，求側面PAB與底面ABCD所成二面角的大小．
  組卷：295引用：2難度：0.5

  解析

• 22．某工藝品加工廠生產線一天能生產200件某款產品，該產品市場評級規定：工藝質量指標值大于或等于10的為A等品，小于10的為B等品．廠家將A等品售價定為160元/件，B等品售價定為140元/件．
  如表是檢驗員在現有生產線上隨機抽取的16件產品的工藝質量指標值：
  

  9.95	10.12	9.96	9.96	10.01	9.92	9.98	10.04
  10.26	9.91	10.13	10.02	9.22	10.04	10.05	9.95

  經計算得

  x

  =

  1

  16

  16

  ∑

  i

  =

  1

  x

  i

  =

  9

  .

  97

  ，

  s

  2

  =

  1

  16

  16

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  =

  1

  16

  16

  ∑

  i

  =

  1

  x

  2

  i

  -

  x

  2

  =

  0

  .

  045

  ，其中x_i為抽取的第i件產品的工藝質量指標值，i=1，2，?，16．
  為了提高產品質量，該廠計劃通過增加生產工序來改進生產工藝，已知增加生產工序每年需花費30萬元，改進后該條生產線產能不變，但生產出的每件產品工藝質量指標值均提高0.05．
  （1）若將隨機抽取的16件產品中各等級產品的頻率視為概率，估計改進后該廠的年收益是否增加，并說明理由．（一年按365天計算）
  （2）根據隨機抽取的16件產品的工藝質量指標值，估計改進后該廠一天生產的所有產品的工藝質量指標值的平均數和方差．
  組卷：101引用：2難度：0.5

  解析