2023-2024學年河北省石家莊二十七中九年級（上）期中數學試卷

一、選擇題：（本大題有16個小題，共38分.1～6小題各3分，7～16小題各2分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若

  a

  b

  =

  3

  4

  ，則

  a

  -

  b

  a

  +

  b

  =（　　）

  A． 1 7

  B． - 1 7

  C．7

  D．-7
  組卷：783引用：5難度：0.8

  解析

• 2．若關于x的一元二次方程x²+4x+c=0有兩個不相等的實數根，則c的值可能為（　　）

  A．6

  B．5

  C．4

  D．3
  組卷：2566引用：32難度：0.8

  解析

• 3．下列4×4的正方形網格中，小正方形的邊長均為1，三角形的頂點都在格點上，則在網格圖中的三角形與△ABC相似的是（　　）

  A．

  B．

  C．

  D．
  組卷：1022引用：5難度：0.6

  解析

• 4．如圖，在Rt△ABC中，∠C=90°，AB=25，AC=7，則cosB等于（　　）

  A． 7 24

  B． 31 24

  C． 24 25

  D． 7 25
  組卷：368引用：2難度：0.8

  解析

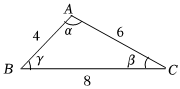• 5．如圖是老師畫出的△ABC，已標出三邊的長度．下面四位同學畫出的三角形與老師畫出的△ABC不一定相似的是（　　）

  A．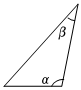

  B．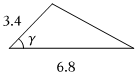

  C．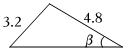

  D．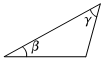
  組卷：937引用：15難度：0.6

  解析

• 6．在△ABC中，若sinA=

  2

  2

  ，cosB=

  1

  2

  ，∠A，∠B都是銳角，則∠C的度數是（　　）

  A．105°

  B．90°

  C．75°

  D．120°
  組卷：734引用：4難度：0.7

  解析

• 7．如圖，在△ABC中，∠ABC=90°，直尺的一邊與BC重合，另一邊分別交AB，AC于點D，E．點B，C，D、E處的讀數分別為15，12，0，1，若直尺寬BD=1cm,則AD的長為（　　）

  A． 1 3 cm

  B． 1 2 cm

  C．1cm

  D． 3 2 cm
  組卷：650引用：6難度：0.6

  解析

• 8．兩千多年前，古希臘數學家歐多克索斯發現了黃金分割，即：如圖，點P是線段AB上一點（AP＞BP），若滿足

  BP

  AP

  =

  AP

  AB

  ，則稱點P是AB的黃金分割點，世界上最有名的建筑物中幾乎都包含“黃金分割”，若圖中AB=8，則BP的長度是（　　）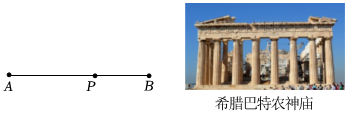
  

  A． 12 - 4 5

  B． 4 + 4 5

  C． 4 5 - 4

  D．2
  組卷：483引用：4難度：0.5

  解析

三、解答題：（共6小題，共72分）

• 25．三亞南山海上觀音圣像是世界上最高的觀音像，某數學實踐小組利用所學的數學知識測量觀音圣像的高度AB，如圖，該數學實踐小組在點C處測得觀音圣像頂端A的仰角為45°，然后沿斜坡CD行走40m到點D處，在點D處測得觀音圣像頂端A的仰角為32°，已知∠ACD=105°．（點A，B，C，D在同一平面內）
  （1）過點D作DE⊥BC交BC的延長線于點E，則∠DCE=

  °；
  （2）填空：DE=

  m,CE=

  m；（結果精確到1m,參考數據：

  2

  ≈1.4，

  3

  ≈1.7）
  （3）求三亞南山海上觀音圣像的高度AB．（結果精確到1m,參考數據：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）
  組卷：406引用：4難度：0.5

  解析

• 26．問題提出：
  
  （1）如圖1，在等腰直角△ABC中，∠BAC=90°，AB=AC，點D、E分別在邊BC、AC上，連接AD、DE，有∠ADE=45°．求證：△BDA∽△CED；
  問題探究
  （2）如圖2，將矩形ABCD沿AE折疊，使點D落在BC邊的點F處，若AB=3，AD=5，求DE的長；
  問題解決
  （3）如圖3，菱形ABCD是一座避暑山莊的平面示意圖，其中∠BAD=60°，AB=120米，現計劃在山莊內修建一個三角形花園AP，點P、Q分別在線段BC、CD上，根據設計要求要使∠APQ=120°，且AP=3PQ，問能否建造出符合要求的三角形花園APQ，若能，請找出點P、Q的位置（即求出DQ與BP的長），若不能，請說明理由．
  組卷：243引用：5難度：0.2

  解析