當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省揚州市邗江區梅嶺中學教育集團九年級（上）期中數學試卷

發布：2024/4/20 14:35:0

一、選擇題（共8小題，每小題3分，滿分24分）

1．一元二次方程x²-2x-1=0的一次項系數是（　　）
A．1 B．-2 C．-1 D．2
組卷：52引用：2難度：0.9
解析
2．已知⊙O的半徑為2，則⊙O中最長的弦長（　　）
A．2 B．
3
C．4 D．
5
組卷：438引用：2難度：0.7
解析
3．下列四條線段能成比例線段的是（　　）
A．2，3，4，5 B．1，2，3，6
C．1.5，2.5，2，3 D．1，1，2，3
組卷：350引用：4難度：0.9
解析
4．如果關于x的方程（x-4）²=m-1可以用直接開平方法求解，那么m的取值范圍是（　　）
A．m≥1 B．m＞1 C．m＞-1 D．m≥-1
組卷：361引用：2難度：0.8
解析
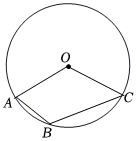5．如圖，點A、B、C在⊙O上，∠AOC=120°，則∠ABC的度數是（　　）
A．100° B．80° C．110° D．120°
組卷：332引用：3難度：0.5
解析
6．某數學興趣小組四人以接龍的方式用配方法解一元二次方程，每人負責完成一個步驟．如圖所示，老師看后，發現有一位同學所負責的步驟是錯誤的，則這位同學是（　　）
A．甲 B．乙 C．丙 D．丁
組卷：599引用：11難度：0.7
解析
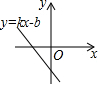7．已知函數y=kx-b的圖象如圖所示，則一元二次方程x²+x+k-1=0根的情況是（　　）
A．沒有實數根 B．有兩個相等的實數根
C．有兩個不相等的實數根 D．不確定
組卷：451引用：5難度：0.7
解析
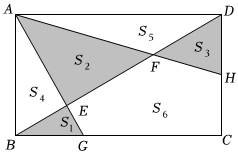8．如圖，在矩形ABCD中，點G是邊BC的三等分點（BG＜GC），點H是邊CD的中點，線段AG，AH與對角線BD分別交于點E，F．設矩形ABCD的面積為S，則以下4個結論中：①FH：AF=1：2；②BE：EF：FD=3：5：4；③S₁+S₂+S₃=
1
3
S：④S₆=S₂+S₅．正確的結論有（　　）
A．1個 B．2個 C．3個 D．4個
組卷：784引用：3難度：0.4
解析

二、填空題（本大題共有10小題，每小題3分，共30分）

9．若
a
b
=
3
2
，則
a
-
b
a
+
b
=
．
組卷：197引用：5難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共有10小題，共96分）

27．閱讀下面材料，回答下列問題：
材料：對于一個關于x的二次三項式ax²+bx+c（a≠0），除了可以利用配方法求該多項式的取值范圍外，還可以利用根的判別式的方法，如下例：
例：求x²+2x+5的最小值；
解：令x²+2x+5=y
∴x²+2x+（5-y）=0
∴Δ=4-4×（5-y）≥0
∴y≥4，∴x²+2x+5的最小值為4．
請利用上述方法解決下列問題：
（1）求代數式-2x²+3x-1的最大值；
（2）若關于x的二次三項式x²+ax+3（a為常數）的最小值為-6，求a的值；
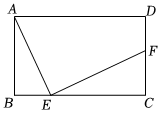
（3）如圖1，矩形ABCD，AB=4，BC=6，點E是邊BC上一動點，連接AE，作EF⊥AE交CD于點F，設BE=x.
①用含x的代數式表示CF的長為
；
②求線段CF長度的取值范圍．
組卷：260引用：2難度：0.5
解析
28．類比推理是根據兩個或兩類對象在一系列屬性上相同或相似，從而推出它們在其他屬性上也相同或相似的推理．借助類比推理可以發現解決問題的方法．
如圖（1），在△ABC中，∠C=90°，
AC
BC
=m,點D、F分別是邊AB、AC上的點，∠B=2∠ADF，過點A作AE⊥DF交DF的延長線于點E，求
AE
DF
的值．
為了獲取解決問題的方法，小敏先假設m=1，點D與點B重合（圖（2）），此時她發現BE是∠ABC的角平分線，因為BE又與AE垂直，所以她想到將AE與BC延長，于是她求出了
AE
DF
的值．
（1）圖（2）中，∠CAE=
°，小敏求出的
AE
DF
=
；
（2）接著在m=1的條件下，她讓點D與點B不重合，如圖（3），請嘗試探究此時
AE
DF
的值；
（3）最后她類比特例中采用的方法，成功地解決的原題．請結合特例探究的經驗，嘗試求出原題圖（1）中
AE
DF
的值．
（4）如圖（4），∠C=90°，點D、F分別在BC、AC邊上，連接AD、BF交于點M，過點A作AE⊥BF，BC=mAF，CF=mBD．請直接寫出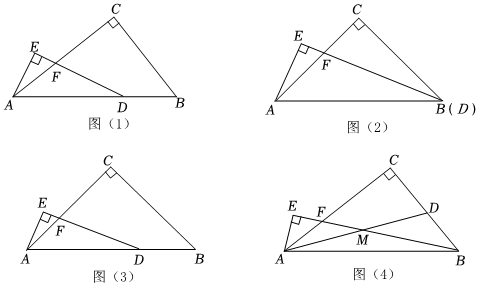
AE
EM
的值．
組卷：277引用：1難度：0.1
解析