當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省廣州六中高二（上）期中數學試卷

發布：2024/10/21 2:0:1

一、單選題

1．若復數
a
+
bi
4
+
3
i
（i為虛數單位，a,b∈R且b≠0）為純虛數，則
a
b
=（　　）
A．
4
3
B．
-
4
3
C．
3
4
D．
-
3
4
組卷：430引用：12難度：0.9
解析
2．“m=-1”是“直線l₁：mx+2y+1=0與直線l₂：
1
2
x
+
my
+
1
2
=0平行”的（　　）
A．充要條件 B．必要不充分條件
C．充分不必要條件 D．既不充分也不必要條件
組卷：1397引用：19難度：0.8
解析
3．數學多選題A，B，C，D四個選項，在給出的選項中，有多項符合題目要求．全都選對的得5分，部分選對的得2分．有選錯的得0分．已知某道數學多選題正確答案為BCD，小明同學不會做這道題目，他隨機地填涂了1個，或2個，或3個選項，則他能得分的概率為（　　）
A．
1
2
B．
7
16
C．
2
5
D．
2
7
組卷：57引用：1難度：0.7
解析
4．已知直線l的方程為
xsinα
+
3
y
-
1
=
0
，α∈R，則直線l的傾斜角范圍是（　　）
A．
（
0
，
π
3
]
∪
[
2
3
π
，
π
）
B．
[
0
，
π
6
]
∪
[
5
π
6
，
π
）
C．
[
π
6
，
5
π
6
]
D．
[
π
3
，
2
π
3
]
組卷：450引用：9難度：0.7
解析
5．設P-ABC是正三棱錐，G是△ABC的重心，D是PG上的一點，且
PD
=
DG
，若
PD
=
x
PA
+
y
PB
+
z
PC
，則（x,y,z）為（　　）
A．
（
5
6
，
1
3
，
2
3
）
B．
（
1
6
，
1
6
，
1
6
）
C．
（
1
6
，
1
3
，
1
3
）
D．
（
1
3
，
5
6
，
1
3
）
組卷：174引用：2難度：0.6
解析
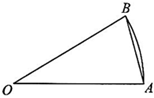6．如圖是一個近似扇形的湖面，其中OA=OB=r,弧AB的長為l（l＜r）．為了方便觀光，欲在A，B兩點之間修建一條筆直的走廊AB．若當0＜x＜
1
2
時，sinx≈x-
x
3
6
，扇形OAB的面積記為S，則
AB
S
的值約為（　　）
A．．
2
l
-
r
2
12
l
3
B．．
2
r
-
l
2
12
r
3
C．．
1
l
-
r
2
24
l
3
D．．
1
r
-
l
2
24
r
3
組卷：147引用：5難度：0.6
解析
7．設A，B，C，D是同一個半徑為2的球的球面上四點，△ABC是以為BC底邊的等腰三角形，且面積為
3
3
4
，
∠
BAC
=
120
°
，則三棱錐D-ABC體積的最大值為（　　）
A．
9
3
2
B．
3
3
C．
9
3
4
D．
3
3
4
組卷：240引用：4難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共70分）

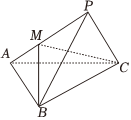21．如圖，三棱錐P-ABC中，
AB
=
BC
=
5
，AC=2，
PA
=
PC
=
6
，
PB
=
17
．
（1）求三棱錐P-ABC的體積；
（2）若點M在棱AP上，且直線CM與平面ABC所成角的正弦值為
21
21
，求二面角M-BC-P所成角的余弦值．
組卷：68引用：4難度：0.5
解析
22．已知O為坐標原點，對于函數f（x）=asinx+bcosx,稱向量
OM
=
（
a
,
b
）
為函數f（x）的伴隨向量，同時稱函數f（x）為向量
OM
的伴隨函數．
（1）設函數
g
（
x
）
=
sin
（
x
+
2
π
3
）
+
cos
（
3
π
2
+
x
）
，試求g（x）的伴隨向量
OM
；
（2）記向量
ON
=
（
1
，
3
）
的伴隨函數為f（x），求當
f
（
x
）
=
6
5
且
x
∈
（
-
π
3
，
π
6
）
時，sinx的值；
（3）當向量
OM
=
（
2
2
，
2
2
）
時，伴隨函數為f（x），函數h（x）=f（2x），求h（x）在區間
[
t
,
t
+
π
4
]
上最大值與最小值之差的取值范圍．
組卷：82引用：10難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．充要條件	B．必要不充分條件
C．充分不必要條件	D．既不充分也不必要條件

A．（ 0 ， π 3 ] ∪ [ 2 3 π ， π ）	B． [ 0 ， π 6 ] ∪ [ 5 π 6 ， π ）
C． [ π 6 ， 5 π 6 ]	D． [ π 3 ， 2 π 3 ]

2023-2024學年廣東省廣州六中高二（上）期中數學試卷

一、單選題

1．若復數a+bi4+3i（i為虛數單位，a,b∈R且b≠0）為純虛數，則ab=（ ）

2．“m=-1”是“直線l1：mx+2y+1=0與直線l2：12x+my+12=0平行”的（ ）

4．已知直線l的方程為xsinα+3y-1=0，α∈R，則直線l的傾斜角范圍是（ ）

5．設P-ABC是正三棱錐，G是△ABC的重心，D是PG上的一點，且PD=DG，若PD=xPA+yPB+zPC，則（x,y,z）為（ ）

6．如圖是一個近似扇形的湖面，其中OA=OB=r,弧AB的長為l（l＜r）．為了方便觀光，欲在A，B兩點之間修建一條筆直的走廊AB．若當0＜x＜12時，sinx≈x-x36，扇形OAB的面積記為S，則ABS的值約為（ ）

7．設A，B，C，D是同一個半徑為2的球的球面上四點，△ABC是以為BC底邊的等腰三角形，且面積為334，∠BAC=120°，則三棱錐D-ABC體積的最大值為（ ）

四、解答題（共70分）

21．如圖，三棱錐P-ABC中，AB=BC=5，AC=2，PA=PC=6，PB=17．（1）求三棱錐P-ABC的體積；（2）若點M在棱AP上，且直線CM與平面ABC所成角的正弦值為2121，求二面角M-BC-P所成角的余弦值．

1．若復數
a
+
bi
4
+
3
i
（i為虛數單位，a,b∈R且b≠0）為純虛數，則
a
b
=（　　）

2．“m=-1”是“直線l₁：mx+2y+1=0與直線l₂：
1
2
x
+
my
+
1
2
=0平行”的（　　）

4．已知直線l的方程為
xsinα
+
3
y
-
1
=
0
，α∈R，則直線l的傾斜角范圍是（　　）

5．設P-ABC是正三棱錐，G是△ABC的重心，D是PG上的一點，且
PD
=
DG
，若
PD
=
x
PA
+
y
PB
+
z
PC
，則（x,y,z）為（　　）

6．如圖是一個近似扇形的湖面，其中OA=OB=r,弧AB的長為l（l＜r）．為了方便觀光，欲在A，B兩點之間修建一條筆直的走廊AB．若當0＜x＜
1
2
時，sinx≈x-
x
3
6
，扇形OAB的面積記為S，則
AB
S
的值約為（　　）

7．設A，B，C，D是同一個半徑為2的球的球面上四點，△ABC是以為BC底邊的等腰三角形，且面積為
3
3
4
，
∠
BAC
=
120
°
，則三棱錐D-ABC體積的最大值為（　　）

21．如圖，三棱錐P-ABC中，
AB
=
BC
=
5
，AC=2，
PA
=
PC
=
6
，
PB
=
17
．
（1）求三棱錐P-ABC的體積；
（2）若點M在棱AP上，且直線CM與平面ABC所成角的正弦值為
21
21
，求二面角M-BC-P所成角的余弦值．