2023-2024學年山東省濟南市鋼城區九年級（上）期中數學試卷（五四學制）

一、選擇題（本題共10小題，每小題選對得4分，選錯、不選或選出的答案超過一個均記零分，共40分）

• 1．已知∠α=30°，則sinα的值是（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D．1
  組卷：20引用：4難度：0.9

  解析

• 2．下列函數是二次函數的是（　　）

  A．y=3x

  B． y = 3 x

  C．y=3x2

  D． y = 3 x 2
  組卷：187引用：2難度：0.9

  解析

• 3．若反比例函數

  y

  =

  -

  6

  x

  的圖象一定經過的點是（　　）

  A．（-1，-6）

  B．（1，6）

  C．（-6，-1）

  D．（1，-6）
  組卷：337引用：5難度：0.6

  解析

• 4．對于二次函數y=（x-1）²+2的圖象，下列說法正確的是（　　）

  A．開口向下	B．對稱軸是直線x=-1
  C．頂點坐標是（1，2）	D．最大值是2
  組卷：781引用：8難度：0.7

  解析

• 5．在同一平面直角坐標系中，函數y=kx+1與y=

  k

  x

  （k≠0）的圖象大致是（　　）

  A．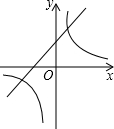

  B．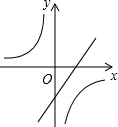

  C．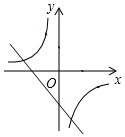

  D．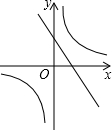
  組卷：1691引用：7難度：0.7

  解析

• 6．下表是小明通過計算得到的函數y=x²-x-5的幾組對應值，則方程x²-x-5=0的一個實數根可能是（　　）
  

  x	-1.5	-1.7	-1.9	-2.1
  y	-1.25	-0.41	0.51	1.51

  A．x≈-1.6

  B．x≈-1.8

  C．x≈-1.95

  D．x≈-2.2
  組卷：192引用：4難度：0.5

  解析

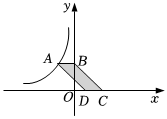• 7．如圖，點A是反比例函數

  y

  =

  -

  6

  x

  的圖象上一點，過點A作AB垂直于y軸，C，D在x軸上，AD∥BC，則平行四邊形ABCD的面積是（　　）

  A．3

  B．6

  C．12

  D．24
  組卷：1429引用：7難度：0.5

  解析

• 8．將二次函數y=（x-2）²+1的圖象繞點（2，1）旋轉180°得到的圖象滿足的解析式為（　　）

  A．y=（x-2）2+1	B．y=（x+2）2+1
  C．y=-（x-2）2+1	D．y=-（x+2）2-1
  組卷：193引用：5難度：0.5

  解析

三、解答題（本大題共10小題，共86分，解答要寫出必要的文字說明、證明過程或推演步驟）

• 25．我們知道，一次函數y=x+1的圖象可以由正比例函數y=x的圖象向左平移1個單位得到；愛動腦的小聰認為：函數y=

  2

  x

  +

  1

  也可以由反比例函數y=

  2

  x

  通過平移得到，小明通過研究發現，事實確實如此，并指出了平移規律，即只要把y=

  2

  x

  （雙曲線）的圖象向左平移1個單位（如圖1虛線所示），同時函數y=

  2

  x

  +

  1

  的圖象上下都無限逼近直線x=-1．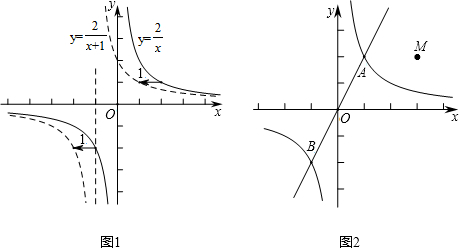
  
  如圖2，已知反比例函數C：y=

  k

  1

  x

  與正比例函數L：y=k₂x的圖象相交于點A（1，2）和點B．
  （1）寫出點B的坐標，并求k₁和k₂的值；
  （2）將函數y=

  k

  1

  x

  的圖象C與直線L同時向右平移n（n＞0）個單位長度，得到的圖象分別記為C′和L′，已知圖象L′經過點M（3，2）；
  則①n的值為

  ；②寫出平移后的圖象C′對應的函數關系式為

  ；
  ③利用圖象，直接寫出不等式

  2

  x

  -

  2

  ＞2x-4的解集為

  ．
  組卷：567引用：5難度：0.5

  解析

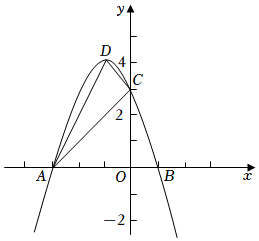• 26．如圖，拋物線y=ax²+bx+c的對稱軸為直線x=-1，與x軸交于A（-3，0），B（1，0）兩點，與y軸交于點C（0，3），設拋物線的頂點為D．
  （1）求拋物線的解析式；
  （2）連接AC、CD、DA，試判斷△ACD的形狀，并說明理由；
  （3）若點Q在拋物線的對稱軸上，拋物線上是否存在點P，使以A、B、Q、P四點為頂點的四邊形為平行四邊形？若存在，請直接寫出滿足條件的點P的坐標；若不存在，請說明理由．
  組卷：524引用：8難度：0.1

  解析