2022-2023學年江蘇省南京師大附中高二（上）期初數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設i是虛數單位，若復數z滿足z（-1+i）=1+i,則復數z=（　　）

  A．i

  B．-i

  C．-1+i

  D．-1-i
  組卷：59引用：2難度：0.9

  解析

• 2．若

  sin

  （

  π

  7

  +

  α

  ）

  =

  1

  2

  ，則

  sin

  （

  3

  π

  14

  -

  2

  α

  ）

  =（　　）

  A． 3 5

  B．- 1 2

  C． 1 2

  D． 1 3
  組卷：380引用：9難度：0.7

  解析

• 3．

  a

  =

  -

  lo

  g

  1

  3

  2

  ，

  b

  =

  3

  log

  2

  1

  3

  ，

  c

  =

  2

  lo

  g

  1

  2

  3，則a,b,c的大小關系是（　　）

  A．c＜a＜b

  B．a＜b＜c

  C．a＜c＜b

  D．c＜b＜a
  組卷：210引用：3難度：0.7

  解析

• 4．設a＞0，b＞0，則“

  1

  a

  +

  1

  b

  ≤4”是“ab≥

  1

  4

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：122引用：5難度：0.7

  解析

• 5．如圖，在坡度一定的山坡A處測得山頂上一建筑物CD的頂端C對于山坡的斜度為15°，向山頂前進100m到達B處，在B處測得C對于山坡的斜度為45°．若CD=50m,山坡對于地平面的坡度為θ，則cosθ等于（　　）

  A． 3 2

  B． 2 2

  C． 3 - 1

  D． 2 - 1
  組卷：314引用：14難度：0.7

  解析

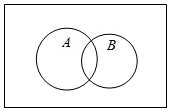• 6．已知一個古典概型的樣本空間Ω和事件A，B如圖所示．其中n（Ω）=12，n（A）=6，n（B）=4，n（A∪B）=8，則事件A與事件

  B

  （　　）

  A．是互斥事件，不是獨立事件

  B．不是互斥事件，是獨立事件

  C．既是互斥事件，也是獨立事件

  D．既不是互斥事件，也不是獨立事件
  組卷：1006引用：7難度：0.9

  解析

• 7．已知△ABC是邊長為2的等邊三角形，D、E分別是AC、AB上的兩點，且

  AE

  =

  EB

  ，

  AD

  =

  2

  DC

  ，BD與CE交于點O，則下列說法錯誤的是（　　）

  A． AB ? CE = 0

  B． OE + OC = 0

  C． | OA + OB + OC | = 3 2

  D． ED 在 BC 方向上的投影向量的模為1
  組卷：188引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．甲、乙兩人玩一個游戲，規則如下：一個袋子中有4個大小和質地完全相同的小球，其中2個紅球，2個白球，甲采取不放回方式從中依次隨機地取出2個球，然后讓乙猜，若乙地猜測與摸出的球特征相符，則乙獲勝，否則甲獲勝，一輪游戲結束，然后進行下一輪（每輪游戲都由甲摸球），乙所要猜的方案從以下兩種猜法中選擇一種．
  猜法一：猜“第二次取出的球是紅球”；
  猜法二：猜“兩次取出球的顏色不同”．
  請回答
  （1）如果你是乙，為了盡可能獲勝，你將選擇哪種猜法，并說明理由；
  （2）假定每輪游戲結果相互獨立，規定有人首先獲勝兩次則為游戲獲勝方，且整個游戲停止，若乙按照（1）中的選擇猜法進行游戲，求乙獲得游戲勝利的概率．
  組卷：188引用：3難度：0.7

  解析

• 22．已知函數f（x）=x²+ax+b,a,b∈R，f（1）=0．
  （1）若函數y=|f（x）|在[0，1]上是減函數，求實數a的取值范圍；
  （2）設F（x）=f（|2^x-1|）+a（|2^x-1|-2），若函數F（x）有三個不同的零點，求實數a的取值范圍；
  （3）是否存在整數m,n,使得m≤f（x）≤n的解集恰好是[m,n]，若存在，求出m,n的值；若不存在，請說明理由．
  組卷：287引用：4難度：0.3

  解析