2017-2018學(xué)年上海市閔行區(qū)七寶中學(xué)高三（下）開學(xué)數(shù)學(xué)試卷

一、填空題

• 1．向量

  a

  =（3，4）在向量

  b

  =（1，-1）方向上的投影為

  ．
  組卷：798引用：13難度：0.9

  解析

• 2．若橢圓mx²+y²=1的一個(gè)焦點(diǎn)與拋物線y²=4x的焦點(diǎn)重合，則m=

   

  ．
  組卷：207引用：2難度：0.7

  解析

• 3．已知集合M={x|x≤a}，N={-2，0，1}，若M∩N={-2，0}，則實(shí)數(shù)a的取值范圍是

   

  ．
  組卷：77引用：3難度：0.9

  解析

• 4．設(shè)無窮等比數(shù)列{a_n}的公比為q,若{a_n}的各項(xiàng)和等于q,則首項(xiàng)a₁的取值范圍是

  ．
  組卷：208引用：5難度：0.9

  解析

• 5．若函數(shù)f（x）=|x+1|+|2x+a|的最小值是3，則正實(shí)數(shù)a的值是

  ．
  組卷：117引用：1難度：0.5

  解析

• 6．將函數(shù)

  f

  （

  x

  ）

  =

  3	cosx
  1	sinx

  按向量

  a

  =

  （

  m

  ,

  0

  ）

  平移（m＞0），若所得圖象對(duì)應(yīng)的函數(shù)為偶函數(shù)，則m的最小值是

  ．
  組卷：26引用：1難度：0.8

  解析

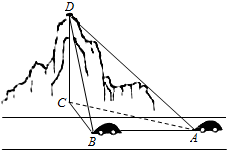• 7．如圖，一輛汽車在一條水平的公路上向正西行駛，到A處時(shí)測(cè)得公路北側(cè)一山頂D在西偏北30°的方向上，行駛600m后到達(dá)B處，測(cè)得此山頂D在西偏北75°的方向上，仰角為30°，則此山的高度CD=

  m.
  組卷：397引用：10難度：0.5

  解析

三、解答題

• 20．已知雙曲線C過點(diǎn)

  （

  4

  ，

  3

  ）

  ，且漸近線方程為

  y

  =±

  1

  2

  x

  ，直線l與曲線C交于點(diǎn)M、N兩點(diǎn)．
  （1）求雙曲線C的方程；
  （2）若直線l過原點(diǎn)，點(diǎn)P是曲線C上任一點(diǎn)，直線PM，PN的斜率都存在，記為k_PM、k_PN，試探究k_PM?k_PN的值是否與點(diǎn)P及直線l有關(guān)，并證明你的結(jié)論；
  （3）若直線l過點(diǎn)（1，0），問在x軸上是否存在定點(diǎn)Q，使得

  QM

  ?

  QN

  為常數(shù)？若存在，求出點(diǎn)Q坐標(biāo)及此常數(shù)的值；若不存在，說明理由．
  組卷：166引用：1難度：0.3

  解析

• 21．已知數(shù)列{a_n}各項(xiàng)不為0，前n項(xiàng)和為S_n．
  （1）若

  S

  n

  +

  a

  n

  =

  4

  ，

  n

  ∈

  N

  *

  ，求數(shù)列{a_n}的通項(xiàng)公式；
  （2）在（1）的條件下，已知b_n=log₂a_n，分別求

  f

  （

  n

  ）

  =

  a

  1

  C

  1

  n

  +

  a

  2

  C

  2

  n

  +

  …

  +

  a

  k

  C

  k

  n

  +

  …

  +

  a

  n

  C

  n

  n

  （

  n

  ∈

  N

  *

  ）

  和

  g

  （

  n

  ）

  =

  b

  1

  C

  1

  n

  +

  b

  2

  C

  2

  n

  +

  …

  +

  b

  k

  C

  k

  n

  +

  …

  +

  b

  n

  C

  n

  n

  （

  n

  ∈

  N

  *

  ）

  的表達(dá)式；
  （3）證明：{a_n}是等差數(shù)列的充要條件是：對(duì)任意n∈N^*，都有：

  1

  a

  1

  a

  2

  +

  1

  a

  2

  a

  3

  +

  …

  +

  1

  a

  n

  a

  n

  +

  1

  =

  n

  a

  1

  a

  n

  +

  1

  ．
  組卷：42引用：1難度：0.4

  解析