2022-2023學年重慶九龍坡區重慶育才中學八年級（上）月考數學試卷（12月份）

一、選擇題：共12小題，每小題5分，每小題的四個選項中，只有一項符合題目要求。

• 1．如果等式（2x-3）^x+3=1，則等式成立的x的值的個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：2075引用：9難度：0.7

  解析

• 2．下列快遞圖標中，是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：114引用：5難度：0.9

  解析

• 3．下列運算正確的（　　）

  A．3a-a=2

  B．a?a2=a3

  C．a6÷a3=a2

  D．（a2）3=a5
  組卷：44引用：3難度：0.7

  解析

• 4．使分式

  x

  2

  -

  1

  x

  +

  1

  等于0的x的值是（　　）

  A．1

  B．-1

  C．±1

  D．不存在
  組卷：67引用：1難度：0.9

  解析

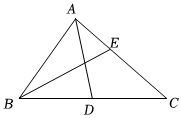• 5．在△ABC中，AD為中線，BE為角平分線，則在以下等式中：（1）∠BAD=∠CAD；（2）∠ABE=∠CBE；（3）BD=DC；（4）AE=EC，其中正確的是（　　）

  A．（1）（2）

  B．（3）（4）

  C．（1）（4）

  D．（2）（3）
  組卷：329引用：1難度：0.6

  解析

• 6．已知10^x=m,5^x=n,則2^x的值為（　　）

  A．mn

  B． m n

  C． n m

  D．m+n
  組卷：356引用：2難度：0.7

  解析

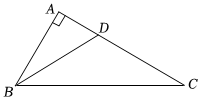• 7．如圖，在Rt△ABC中，∠A=90°，∠ABC的平分線交AC于點D，AD=3，BC=10，則△BDC的面積是（　　）

  A．15

  B．12

  C．30

  D．10
  組卷：104引用：2難度：0.7

  解析

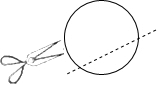• 8．如圖，小明同學用剪刀沿著虛線將一張圓形紙片剪掉一部分，發現剩下紙片的周長比原來的周長要小，能正確解釋這一現象的數學知識是（　　）

  A．兩點之間，直線最短

  B．經過一點，有無數條直線

  C．兩點確定一條直線

  D．兩點之間，線段最短
  組卷：606引用：12難度：0.9

  解析

三、解答題：70分

• 25．觀察猜想：
  
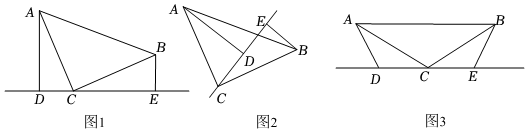
  （1）如圖1，∠ACB=90°，AC=BC，D，C，E三點在同一條直線上，且AD⊥CE，BE⊥CE，垂足分別為點D，E，則線段AD，DE，BE三者之間的數量關系是

  ；
  類比探究：
  （2）如圖2，∠ACB=90°，AC=BC，D，C，E三點在同一條直線上，且AD⊥CE，BE⊥CE，垂足分別為D，E，線段AD，DE，BE三者之間的數量關系有變化嗎？請說明理由；
  拓展延伸：
  （3）如圖3，若將（1）中的條件改為：在△ABC中，AC=BC，D，C，E三點在同一條直線上，并且有∠BEC=∠ADC=∠BCA=α，α為任意鈍角，那么（1）中你的結論是否還成立？若成立，請證明；若不成立，請說明理由．
  組卷：187引用：3難度：0.2

  解析

• 26．閱讀理解應用．
  待定系數法：設某一多項式的全部或部分系數為未知數、利用當兩個多項式為恒等式時，同類項系數相等的原理確定這些系數，從而得到待求的值．
  待定系數法可以應用到因式分解中，例如問題：因式分解x³-1．
  因為x³-1為三次多項式，若能因式分解，則可以分解成一個一次多項式和一個二次多項式的乘積．
  故我們可以猜想x³-1可以分解成x³-1=（x-1）（x²+ax+b），展開等式右邊得：x³+（a-1）x²+（b-a）x-b,根據待定系數法原理，等式兩邊多項式的同類項的對應系數相等：a-1=0，b-a=0，-b=-1，可以求出a=1，b=1．
  所以x³-1=（x-1）（x²+x+1）．
  （1）若x取任意值，等式x²+2x+3=x²+（3-a）x+3恒成立，則a=

  ；
  （2）已知多項式x⁴+x²+1有因式x²+x+1，請用待定系數法求出該多項式的另一因式；
  （3）請判斷多項式x⁴-x²+1是否能分解成的兩個整系數二次多項式的乘積，并說明理由．
  組卷：419引用：3難度：0.7

  解析