2022-2023學年重慶市南開中學高二(上)期末數學試卷
發布:2024/12/31 2:30:2
一、單選題(本題共8小題,每小題5分,共40分.在每小題給出的選項中,只有一項符合題目要求)
-
1.已知f'(x)是函數
的導函數,則f(x)=sinx-sinπ6=( )f′(π6)A. -12B. -32C. 12D. 32組卷:362引用:1難度:0.8 -
2.在等差數列{an}中,若a3+a17=30,則a9+a10+a11=( )
A.30 B.40 C.45 D.60 組卷:600引用:2難度:0.9 -
3.已知拋物線x2=2py(p>0),若拋物線上縱坐標為2的點到焦點的距離為3,則p=( )
A. 12B.1 C.2 D.3 組卷:186引用:1難度:0.8 -
4.音樂與數學有著密切的聯系,我國春秋時期有個著名的“三分損益法”:若以“宮”為基本音,“宮”經過一次“損”,頻率變為原來的
,得到“徵”;“徵”經過一次“益”,頻率變為原來的54,得到“商”;依次損益交替變化,獲得了“宮、徵、商、羽、角”五個音階.據此可推得( )12A.“徵、商、羽”的頻率成等比數列 B.“宮、徵、商”的頻率成等比數列 C.“商、羽、角”的頻率成等比數列 D.“宮、商、角”的頻率成等比數列 組卷:132引用:4難度:0.8 -
5.設函數
在(1,2)上單調遞減,則實數a的取值范圍是( )f(x)=2x-2x-alnxA.[4,5] B.(5,+∞) C.[4,+∞) D.[5,+∞) 組卷:1043引用:8難度:0.7 -
6.法國數學家加斯帕爾?蒙日發現:與橢圓
相切的兩條互相垂直的直線的交點軌跡是以橢圓中心為圓心的圓x2+y2=a2+b2,我們通常把這個圓稱為該橢圓的蒙日圓.若圓x2a2+y2b2=1(a>b>0)上存在點P,使得過點P可作兩條互相垂直的直線與橢圓C:(x-a)2+(y-3a)2=4(a∈R)相切,則實數a的取值范圍為( )x23+y2=1A.[0,2] B.[-2,2] C.[0,4] D.[-4,4] 組卷:156引用:3難度:0.7 -
7.若數列{an}滿足a1=1,a2=4,且對于n∈N*(n≥2)都有an+1=2an-an-1+2,則
=( )1a2-1+1a4-1+1a6-1+?+1a2022-1A. 20212022B. 10102022C. 20222023D. 10112023組卷:182引用:2難度:0.6
四.解答題(本大題共70分,解答應寫出文字說明、證明過程或演算步驟)
-
21.已知函數f(x)=ex(x2+2ax+2a)(a∈R),其中e是自然對數的底數.
(1)討論函數f(x)的單調性;
(2)若在區間[-2,0]上有解,求實數a的取值范圍.f(x)≤ae2組卷:394引用:1難度:0.6 -
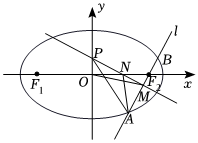 22.已知橢圓的左右焦點為F1、F2,且|F1F2|=4,直線l過C:x2a2+y2b2=1(a>b>0)
22.已知橢圓的左右焦點為F1、F2,且|F1F2|=4,直線l過C:x2a2+y2b2=1(a>b>0)
F2且與橢圓C相交于A,B兩點,當F2是線段AB的中點時,.|AB|=263
(1)求橢圓C的標準方程;
(2)當線段AB的中點M不在x軸上時,設線段AB的中垂線與x軸交于點N,與y軸交于點P,O為橢圓的中心,記△OMN的面積為S1,△APM的面積為S2,當取得最大值時,求直線l的方程.S1S2組卷:118引用:1難度:0.3


