2021-2022學年廣東省深圳外國語學校龍華中學高中部高一（上）期中數學試卷

一、單項選擇題（本題共8小題，每題4分，共32分）

• 1．已知集合A={x|-1≤x＜5，x∈Z}，B={-1，1，3，5}，則A∩B=（　　）

  A．?	B．{-1，1，3}
  C．{-1，1，3，5}	D．{-1，0，1，2，3，4，5}
  組卷：31引用：3難度：0.7

  解析

• 2．命題“?x₀∈R，

  x

  2

  0

  +

  3

  x

  0

  -

  2

  =

  0

  ”的否定為（　　）

  A．?x∈R，x2+3x-2=0	B．?x∈R，x2+3x-2≠0
  C．?x1∈R， x 2 1 + 3 x 2 1 - 2 = 0	D．?x1∈R， x 2 1 + 3 x 2 1 - 2 ≠ 0
  組卷：141引用：5難度：0.8

  解析

• 3．設a、b、c為實數，且a＜b＜0，則下列不等式正確的是（　　）

  A． 1 a ＜ 1 b

  B．ac2＜bc2

  C． b a ＞ a b

  D．|a|＞|b|
  組卷：326引用：4難度：0.9

  解析

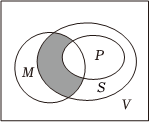• 4．如圖所示，兩個大圓和一個小圓分別表示集合M、S、P，它們是V的三個子集，則陰影部分所表示的集合是（　　）

  A．（M∩P）∩S	B．（M∩P）∪S
  C．（M∩S）∩（?SP）	D．（M∩P）∪（?VS）
  組卷：60引用：3難度：0.7

  解析

• 5．

  x

  2

  +

  4

  x

  2

  +

  1

  的最小值等于（　　）

  A．3

  B． 5 2

  C．2

  D．無最小值
  組卷：77引用：3難度：0.7

  解析

• 6．十九世紀下半葉集合論的創立．奠定了現代數學的基礎．著名的“康托三分集．（Cantor）”是數學理性思維的構造產物，具體典型的分形特征，其操作過程如下：將閉區間[0，1]均分為三段，去掉中間的開區間段（

  1

  3

  ，

  2

  3

  ），記為第一次操作；再將剩下的兩個區間

  [

  0

  ，

  1

  3

  ]

  ，

  [

  2

  3

  ，

  1

  ]

  分別均分為三段，并各自去掉中間的開區間段，記為第二次操作；……如此這樣，每次在上一次操作的基礎上，將剩下的各個區間分別均分為三段，同樣各自去掉中間的開區間段．操作過程不斷地進行下去．以至無窮，剩下的區間集合即“康托三分集”．第三次操作后，從左到右第四個區間為（　　）

  A．[ 2 9 ， 1 3 ]

  B．[ 2 27 ， 1 9 ]

  C．[ 8 27 ， 1 3 ]

  D．[ 8 9 ， 25 27 ]
  組卷：23引用：3難度：0.5

  解析

• 7．定義在R上的偶函數f（x）在[0，+∞）單調遞減，則不等式f（a-2）＞f（1）的解集是（　　）

  A．（-∞，3）

  B．（3，+∞）

  C．（-1，3）

  D．（1，3）
  組卷：38引用：4難度：0.7

  解析

四、解答題（解答應寫出必要的文字說明、證明過程或演算步驟）

• 21．已知函數f（x）是定義在R上的奇函數，且當x≥0時，f（x）=x²-2x.
  （1）求函數f（x）的解析式并畫出其圖像；
  （2）設函數f（x）在[-2，a]，（a＞-2）上的最大值為g（a），求g（a）．
  組卷：73引用：5難度：0.5

  解析

• 22．對于定義域為D的函數f（x），若同時滿足下列條件：
  ①f（x）在D內是單調函數；
  ②存在區間[a,b]?D，使f（x）在區間[a,b]上的值域也為[a,b]，則稱f（x）為D上的精彩函數，[a,b]為函數f（x）的精彩區間．
  （1）寫出一個具體的精彩函數及其精彩區間；
  （2）函數

  f

  （

  x

  ）

  =

  x

  +

  1

  x

  （

  x

  ≥

  1

  ）

  ，判斷f（x）是否為精彩函數？若是，求出其精彩區間；若不是，請說明理由；
  （3）若函數

  g

  （

  x

  ）

  =

  x

  +

  4

  +

  m

  是精彩函數，求實數m的取值范圍．
  組卷：38引用：2難度：0.4

  解析