當前位置：試卷中心 > 試卷詳情

2022-2023學年浙江省湖州市吳興區八年級（下）期中數學試卷

發布：2024/7/5 8:0:9

一、選擇題（每題3分，本大題共10小題，共30分）

1．若x為任意實數，下列各式一定是二次根式的是（　　）
A．
x
2
-
3
B．
2
（
x
+
1
）
2
C．
x
2
+
1
D．
x
2
+
2
x
組卷：803難度：0.7
解析
2．下面的圖形是用數學家名字命名的，其中既是軸對稱圖形又是中心對稱圖形的是（　　）
A．
斐波那契螺旋線 B．
笛卡爾心形線
C．
趙爽弦圖 D．
科克曲線
組卷：1184引用：74難度：0.8
解析
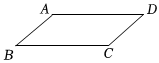3．如圖，在平行四邊形ABCD中，∠A：∠B=7：2，則∠A的度數是（　?。?/h2>
A．110° B．140° C．120° D．160°
組卷：123引用：2難度：0.8
解析
4．下列根式中，不是最簡二次根式的是（　　）
A．
5
B．
8
C．
2
2
D．
6
組卷：317引用：9難度：0.8
解析
5．有一組數據：2，5，5，6，7，這組數據的平均數為（　?。?/h2>
A．3 B．4 C．5 D．6
組卷：1229引用：25難度：0.9
解析
6．用配方法解一元二次方程x²-2x-5=0，下列配方正確的是（　　）
A．（x+1）²=6 B．（x+1）²=9 C．（x-1）²=9 D．（x-1）²=6
組卷：319引用：10難度：0.9
解析
7．用反證法證明命題：“等腰三角形的底角是銳角”時，第一步可以假設（　?。?/h2>
A．等腰三角形的底角是直角
B．等腰三角形的底角是直角或鈍角
C．等腰三角形的底角是鈍角
D．底角為銳角的三角形是等腰三角形
組卷：186引用：3難度：0.8
解析
8．若m是關于x的方程x²-2023x-1=0的根，則（m²-2023m+3）?（m²-2023m+4）的值為（　　）
A．16 B．12 C．20 D．30
組卷：510引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共8小題，共66分.）

23．閱讀下列材料，解答后面的問題：
在二次根式的學習中，我們不僅要關注二次根式本身的性質、運算，還要用到與分式、不等式相結合的一些運算．如：
①要使二次根式
a
-
2
有意義，則需a-2≥0，解得：a≥2；
②化簡：
1
+
1
n
2
+
1
（
n
+
1
）
2
，則需計算
1
+
1
n
2
+
1
（
n
+
1
）
2
，而
1
+
1
n
2
+
1
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
（
n
+
1
）
2
+
n
2
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
n
2
+
2
n
+
1
+
n
2
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
2
n
2
+
2
n
+
1
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
2
n
（
n
+
1
）
+
1
n
2
（
n
+
1
）
2
=
[
n
（
n
+
1
）
+
1
]
2
n
2
（
n
+
1
）
2
所以
1
+
1
n
2
+
1
（
n
+
1
）
2
=
[
n
（
n
+
1
）
+
1
]
2
n
2
（
n
+
1
）
2
=
n
（
n
+
1
）
+
1
n
（
n
+
1
）
=
1
+
1
n
（
n
+
1
）
=
1
+
1
n
-
1
n
+
1
．
（1）根據二次根式的性質，要使
a
+
2
3
-
a
=
a
+
2
3
-
a
成立，求a的取值范圍；
（2）利用①中的提示，請解答：如果
b
=
a
-
2
+
2
-
a
+
1
，求a+b的值；
（3）利用②中的結論，計算：
1
+
1
1
2
+
1
2
2
+
1
+
1
2
2
+
1
3
2
+
1
+
1
3
2
+
1
4
2
+
?
+
1
+
1
2022
2
+
1
2023
2
．
組卷：157引用：1難度：0.6
解析
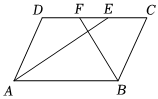24．問題：如圖，在平行四邊形ABCD中，AB=10，AD=6，∠DAB，∠ABC的平分線AE、BF分別與直線CD交于點E、F，請直接寫出EF的長．
探究：（1）把“問題”中的條件“AB=10”去掉，其余條件不變．
①當點E與點F重合時，AB的長為
．
②當點E與點C重合時，EF的長為
．
（2）把“問題”中的條件“AB=10，AD=6”去掉，其余條件不變，當點C，D，E，F相鄰兩點間的距離相等時，求
AD
AB
的值．
組卷：538引用：3難度：0.5
解析