當前位置：試卷中心 > 試卷詳情

2010年數學奧林匹克模擬試卷（20）

發布：2024/4/20 14:35:0

1．計算：
1
3
+
3
+
1
5
3
+
3
5
+
1
7
5
+
5
7
+
…
+
1
81
79
+
79
81
=（　　）
A．
1
3
B．
4
9
C．
5
9
D．
2
3
組卷：588引用：1難度：0.9
解析
2．若
1
x
＜
2
，
1
x
＞
-
3
，則x的取值范圍（　　）
A．
-
1
3
＜
x
＜
1
2
B．
-
1
3
＜
x
＜
0
或
x
＞
1
2
C．
x
＜
-
1
3
或
x
＞
1
2
D．以上答案都不對
組卷：2453引用：5難度：0.5
解析
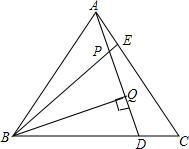3．如圖，點D、E是正△ABC的邊BC、AC上的點，且CD=AE，AD、BE相交于P點，BQ⊥AD于Q，已知PE=1，PQ=3，則AD等于（　　）
A．5 B．6 C．7 D．8
組卷：290引用：6難度：0.7
解析
4．已知實數a、b分別滿足
4
a
4
-
2
a
2
-
3
=
0
和b⁴+b²-3=0，則
a
4
b
4
+
4
a
4
的值為（　　）
A．7 B．8 C．9 D．10
組卷：173引用：1難度：0.9
解析

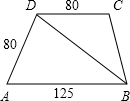12．如圖，梯形ABCD中，AB∥CD，AB=125，AD=DC=80，問對角線BD能否把梯形分成兩個相似的三角形？若不能，給出證明；若能，求出BC、BD的長．
組卷：55引用：1難度：0.5
解析
13．在坐標平面上，橫縱坐標都是整數的點稱為整點，而頂點均為整點的多邊形稱為整點多邊形，求證：整點凸五邊形必可以找到一個四邊形至少覆蓋5個整點．
組卷：77引用：2難度：0.3
解析

A． - 1 3 ＜ x ＜ 1 2	B． - 1 3 ＜ x ＜ 0 或 x ＞ 1 2
C． x ＜ - 1 3 或 x ＞ 1 2	D．以上答案都不對

1．計算：13+3+153+35+175+57+…+18179+7981=（ ）