當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省無錫市四校聯考高一（下）期中數學試卷

發布：2024/8/27 4:0:8

一、單選題（本大題共8小題，每小題只有一個正確選項，每題5分，共40分）

1．已知復數
z
=
2
+
i
1
-
i
，則z?
z
=（　　）
A．1 B．
3
2
C．2 D．
5
2
組卷：65引用：2難度：0.8
解析
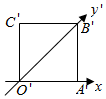2．一個水平放置的平面圖形，用斜二測畫法畫出了它的直觀圖，如圖所示，此直觀圖恰好是一個邊長為2的正方形，則原平面圖形的面積為（　　）
A．
2
B．
4
2
C．8 D．
8
2
組卷：442引用：5難度：0.8
解析
3．一質點在力
F
1
=（-3，5），
F
2
=（2，-3）的共同作用下，由點A（10，-5）移動到B（4，0），則
F
1
，
F
2
的合力
F
對該質點所做的功為（　　）
A．16 B．-24 C．110 D．-110
組卷：197引用：3難度：0.8
解析
4．在△ABC中，a²+b²+c²=2bccosA+2accosB，則△ABC一定是（　　）
A．銳角三角形 B．鈍角三角形 C．直角三角形 D．等邊三角形
組卷：236引用：3難度：0.8
解析
5．中國古代數學家劉徽在《九章算術注》中，稱一個正方體內兩個互相垂直的內切圓柱所圍成的立體為“牟合方蓋”，如圖（1）（2），劉徽未能求得牟合方蓋的體積，直言“欲陋形措意，懼失正理”，不得不說“敢不闕疑，以俟能言者”．約200年后，祖沖之的兒子祖暅提出“冪勢既同，則積不容異”，后世稱為祖暅原理，即：兩等高立體，若在每一等高處的截面積都相等，則兩立體體積相等．如圖（3）（4），祖暅利用八分之一正方體去掉八分之一牟合方蓋后的幾何體與長寬高皆為八分之一正方體的棱長的倒四棱錐“等冪等積”，計算出牟合方蓋的體積，據此可知，牟合方蓋的體積與其外切正方體的體積之比為（　　）
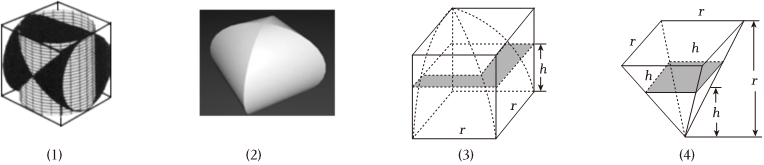
A．
1
3
B．
2
3
C．
8
3
D．
16
3
組卷：172引用：5難度：0.7
解析
6．已知
α
∈
（
0
，
π
2
）
，
sin
2
α
=
cos
（
π
4
-
α
）
，則cos2α的值為（　　）
A．0 B．
1
2
C．
3
2
D．-
3
2
組卷：299引用：5難度：0.6
解析
7．設A₁、A₂、A₃、A₄為平面直角坐標系中兩兩不同的點，若
A
1
A
3
=
λ
A
1
A
2
（
λ
∈
R
）
，
A
1
A
4
=
μ
A
1
A
2
（
μ
∈
R
）
，且
1
λ
+
1
μ
=
4
，則稱點A₃、A₄和諧分割點A₁、A₂.已知平面上兩兩不同的點A、B、C、D，若C、D和諧分割點A、B．則下面說法正確的是（　　）
A．點C可能是線段AB的中點
B．點C可能是靠近點A的線段AB的三等分點
C．點C、D可能同時在線段AB上
D．點C、D可能同時在線段AB的延長線上
組卷：127引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，作答各題時須有必要的計算和推理過程，共70分）

21．如圖所示，在△ABC中，P在線段BC上，滿足2
BP
=
PC
，O是線段AP的中點，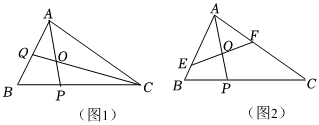

（1）延長CO交AB于點Q（圖1），求
AQ
QB
的值；
（2）過點O的直線與邊AB，AC分別交于點E，F（圖2），設
EB
=
λ
AE
，
FC
=
μ
AF
．
（ⅰ）求證：2λ+μ為定值；
（ⅱ）設△AEF的面積為S₁，△ABC的面積為S₂，求
S
1
S
2
的最小值．
組卷：619引用：5難度：0.2
解析
22．如圖，某公園改建一個三角形池塘，∠C=90°，AB=2百米，BC=1百米，現準備養一批觀賞魚供游客觀賞．

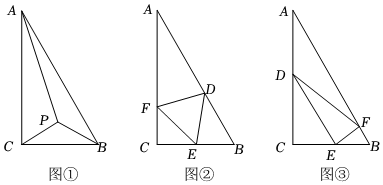
（1）若在△ABC內部取一點P，建造連廊供游客觀賞，方案一如圖①，使得點P是等腰三角形PBC的頂點，且
∠
CPB
=
2
π
3
，求連廊AP+PC+PB的長（單位為百米）；
（2）若分別在AB，BC，CA上取點D，E，F，并建造連廊，使得△DEF變成池中池，放養更名貴的魚類供游客觀賞：方案二如圖②，使得△DEF為正三角形，設S₂為圖②中△DEF的面積，求S₂的最小值；方案三如圖③，使得DE平行于AB，且EF垂直于DE，設S₃為圖③中△DEF的面積，求S₃的取值范圍．
組卷：155引用：4難度：0.7
解析