當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省鹽城市五校高一（下）聯考數學試卷（5月份）

發布：2024/5/24 8:0:9

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知α，β為銳角，
tanα
=
5
12
，
cos
（
α
+
β
）
=
-
10
10
，則tan（α-β）的值為（　　）
A．
477
479
B．
479
477
C．
-
479
241
D．
-
477
241
組卷：141引用：1難度：0.5
解析
2．若復數z滿足（4+2i）z=（3-i）²，則|z|=（　　）
A．1 B．
2
C．
3
D．
5
組卷：59引用：4難度：0.9
解析
3．已知向量
a
=（2，m），
b
=（4，-1），且（
a
-
b
）⊥（
a
+
b
），則實數m=（　　）
A．2 B．
1
2
C．8 D．
±
13
組卷：409引用：5難度：0.7
解析
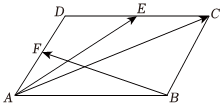4．如圖，四邊形ABCD是平行四邊形，點E，F分別為CD，AD的中點，若以向量
AE
，
BF
為基底表示向量
AC
，則下列結論正確的是?（　　）
A．
AC
=
1
5
AE
+
3
5
BF
B．
AC
=
3
5
AE
-
4
5
BF
C．
AC
=
AE
-
1
5
BF
D．
AC
=
6
5
AE
-
2
5
BF
組卷：293引用：4難度：0.7
解析
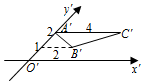5．如圖，△A'B'C'是△ABC用斜二測畫法畫出的直觀圖，則△ABC的周長為（　　）
A．12 B．
2
（
2
+
5
）
C．
4
（
1
+
2
）
D．
2
（
2
+
2
+
5
）
組卷：156引用：3難度：0.7
解析
6．在△ABC中，內角A，B，C的對邊分別為a,b,c,
sin
A
-
sin
B
+
2
a
-
2
b
c
=
0
，則△ABC的一定為（　　）
A．直角三角形 B．等腰三角形 C．等邊三角形 D．鈍角三角形
組卷：108引用：6難度：0.7
解析
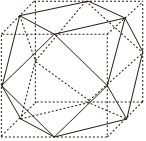7．“阿基米德多面體”被稱為半正多面體（semi-regularsolid），是由邊數不全相同的正多邊形為面圍成的多面體，它體現了數學的對稱美．如圖所示，將正方體沿交于一頂點的三條棱的中點截去一個三棱錐，共可截去八個三棱錐，得到八個面為正三角形、六個面為正方形的一種半正多面體．已知正方體棱長為6，則該半正多面體外接球的表面積為（　　）
A．48π B．56π C．64π D．72π
組卷：630引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

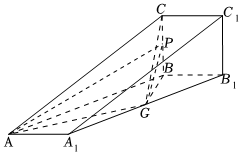21．如圖，三棱柱ABC-A₁B₁C₁的側面BB₁C₁C是邊長為1的正方形，側面BB₁C₁C⊥側面AA₁B₁B，AB=4，∠A₁B₁B=60°，G是A₁B₁的中點．
（1）求證：平面GBC⊥平面BB₁C₁C；
（2）若P為線段BC的中點，求三棱錐A-PBG的體積．
組卷：73引用：2難度：0.5
解析
22．十字測天儀廣泛應用于歐洲中世紀晚期的航海領域，主要用于測量太陽等星體的方位，便于船員確定位置．如圖1所示，十字測天儀由桿AB和橫檔CD構成，并且E是CD的中點，橫檔與桿垂直并且可在桿上滑動．十字測天儀的使用方法如下：如圖2，手持十字測天儀，使得眼睛可以從A點觀察．滑動橫檔CD使得A，C在同一水平面上，并且眼睛恰好能觀察到太陽，此時視線恰好經過點D，DE的影子恰好是AE．然后，通過測量AE的長度，可計算出視線和水平面的夾角∠CAD（稱為太陽高度角），最后通過查閱地圖來確定船員所在的位置．

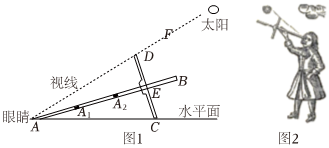
（1）若在某次測量中，橫檔CD的長度為20，測得太陽高度角∠CAD=60°，求影子AE的長；
（2）若在另一次測量中，AE=40，橫檔CD的長度為20，求太陽高度角的正弦值；
（3）在桿AB上有兩點A₁，A₂滿足AA₁=
1
2
A
A
2
．當橫檔CD的中點E位于A_i時，記太陽高度角為a_i（i=1，2），其中α₁，α₂都是銳角．證明：α₁＜2α₂．
組卷：92引用：7難度：0.5
解析