當前位置：試卷中心 > 試卷詳情

2023年內(nèi)蒙古赤峰市高考數(shù)學模擬試卷（理科）（4月份）

發(fā)布：2024/12/4 17:0:2

1．設全集U={1，2，3，4，5，6，7，8}，A∩?_UB={1，3}，?_U（A∪B）={2，4}，則集合B為（　　）
A．{1，3，5，6，7，8} B．{2，4，5，6，7，8}
C．{5，6，7，8} D．{1，2，3，4}
組卷：41引用：2難度：0.7
解析
2．棣莫弗公式[r（cosθ+isinθ）]ⁿ=rⁿ（cosnθ+isinnθ），（i是虛數(shù)單位，r＞0）是由法國數(shù)學家棣莫弗（1667-1754）發(fā)現(xiàn)的．根據(jù)棣莫弗公式，在復平面內(nèi)的復數(shù)
[
2
（
cos
π
4
+
isin
π
4
）
]
11
對應的點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：44引用：1難度：0.8
解析

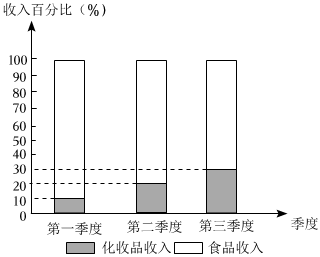3．在“萬眾創(chuàng)業(yè)”的大背景下，“直播電商”已經(jīng)成為我國當前經(jīng)濟發(fā)展的新增長點，已知某電商平臺的直播間經(jīng)營化妝品和食品兩大類商品，2022年前三個季度，該直播間每個季度的收入都比上一個季度的收入翻了一番，其前三季度的收入情況如圖所示，則（　　）

A．該直播間第三季度總收入是第一季度總收入的3倍

B．該直播間第三季度化妝品收入是第一季度化妝品收入的6倍

C．該直播間第三季度化妝品收入是第二季度化妝品收入的3倍

D．該直播間第三季度食品收入低于前兩個季度的食品收入之和

組卷：31引用：2難度：0.6

4．函數(shù)
f
（
x
）
=
xsinx
-
1
x
2
在（-π，0）∪（0，π）上的圖像大致為（　　）
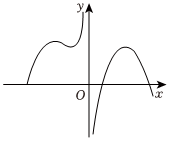
A． B．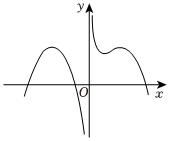
C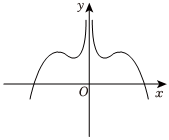． D．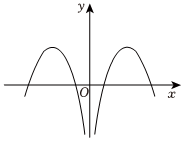
組卷：65引用：2難度：0.7
解析
5．九連環(huán)是中國杰出的益智游戲，九連環(huán)由9個相互連接的環(huán)組成，這9個環(huán)套在一個中空的長形柄中，九連環(huán)的玩法就是要將這9個環(huán)從柄上解下來（或套上），規(guī)則如下：如果要解下（或套上）第n環(huán)，則第n-1號環(huán)必須解下（或套上），n-1往前的都要解下（或套上）才能實現(xiàn)．記解下n連環(huán)所需的最少移動步數(shù)為a_n，已知a₁=1，a₂=2，a_n=a_n-1+2a_n-2+1（n≥3），若要解下7環(huán)最少需要移動圓環(huán)步數(shù)為（　　）
A．42 B．85 C．170 D．341
組卷：62引用：2難度：0.7
解析

A．在△ABC中，p：A＞B，q：sinA＞sinB

B．已知x,y是兩個實數(shù)，p：x²-2x-3≤0，q：0≤x≤2

C．對于兩個實數(shù)x,y,p：x+y≠8，q：x≠3或y≠5

D．兩條直線方程分別是l₁：ax+2y+6=0，l₂：x+（a-1）y+a²-1=0，p：l₁∥l₂，q：a=2或-1

組卷：56引用：2難度：0.7

A．{1，3，5，6，7，8}	B．{2，4，5，6，7，8}
C．{5，6，7，8}	D．{1，2，3，4}

A．	B．
C．	D．