2022-2023學年安徽省池州二中九年級（上）期中數學試卷

一、單選題

• 1．下列y和x之間的函數表達式中，屬于二次函數的是（　　）

  A．y=x2+ 1 x	B．y=2x3+5
  C．y=（x+4）（x-1）	D．y=2x-7
  組卷：114引用：2難度：0.7

  解析

• 2．拋物線y=ax²+bx-3過點（2，4），則代數式8a+4b的值為（　　）

  A．14

  B．2

  C．-2

  D．-14
  組卷：27引用：4難度：0.6

  解析

• 3．若拋物線y=ax²-2ax-2的開口向下，（-2，y₁），（3，y₂），（0，y₃）為拋物線上的三個點，則（　　）

  A．y3＜y2＜y1

  B．y1＜y2＜y3

  C．y3＜y1＜y2

  D．y2＜y3＜y1
  組卷：142引用：4難度：0.6

  解析

• 4．已知反比例函數

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  的圖象經過點（1，-2），則這個函數的圖象一定經過（　　）

  A．（2，1）

  B．（2，-1）

  C．（2，4）

  D．（-1，-2）
  組卷：60引用：6難度：0.7

  解析

• 5．按如圖所示的運算程序，能使輸出y值為3的是（　　）
  

  A．x=1

  B．x=2

  C．x=3

  D．x=4
  組卷：431引用：2難度：0.7

  解析

• 6．在平面直角坐標系xOy中，二次函數y=ax²+bx+c（a≠0的圖象如圖所示，下列結論：①abc＞0；②a-b+c＜0；③2a-b=0；④b²＞4ac；⑤若m為任意實數，則a+b≥am²+bm.其中正確的是（　　）

  A．1個

  B．2 個

  C．3 個

  D．4 個
  組卷：869引用：11難度：0.5

  解析

• 7．直線y=ax+b與拋物線y=ax²+bx+c在同一平面直角坐標系中的圖象可能是（　　）

  A．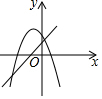

  B．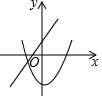

  C．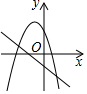

  D．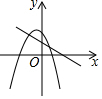
  組卷：834引用：5難度：0.5

  解析

三、解答題

• 22．定義：如果兩個二次函數的圖象的開口大小相同，方向相反且頂點的橫坐標、縱坐標都互為相反數，則稱其中一個二次函數為另一個二次函數的美麗函數．如y=-（x+3）²+2與y=（x-3）²-2互為美麗函數．
  （1）求y=-2x²+4x-1的美麗函數的表達式；
  （2）若y₁=x²+2x+c的圖象的頂點為P，且經過它的美麗函數y₂=-（x+h）²+k的圖象的頂點Q．
  ①求證：這兩個函數的圖象的交點為P，Q；
  ②點M是y₁=x²+2x+c在P，Q之間的圖象的動點，MN⊥x軸交y₂=-（x+h）²+k的圖象于點N，求MN長度的最大值．
  組卷：43引用：3難度：0.5

  解析

• 23．如圖，一次函數y=-2x+6的圖象與y軸交于A點，與x軸交于B點，二次函數y=-x²+bx+c的圖象經過A、B兩點．
  （1）求二次函數的解析式；
  （2）根據圖象直接寫出當x取何值時，-2x+6＞-x²+bx+c＞0；
  （3）點P是拋物線在第一象限上的一個動點，是否存在點P，使△ABP面積最大，若存在，求出此時點P坐標以及△ABP面積，若不存在，請說明理由．
  組卷：503引用：4難度：0.5

  解析