當前位置：試卷中心 > 試卷詳情

2010-2011學年山東省濰坊市三縣高二（下）模塊學分認定考試數學試卷（文科）

發布：2024/4/20 14:35:0

1．已知集合A={x|-1≤x≤2，x∈Z}，集合B={0，2，4}，則A∪B等于（　　）
A．{-1，0，1，2，4} B．{-1，0，2，4} C．{0，2，4} D．{0，1，2，4}
組卷：101引用：9難度：0.9
解析
2．若a,b,c∈R，且a＞b,則下列不等式中恒成立的是（　　）
A．
1
a
＞
1
b
B．ac＞bc C．a²＞b² D．a+c＞b+c
組卷：84引用：6難度：0.9
解析
3．函數f（x）=
lg
|
x
|
x
的圖象可能是（　　）
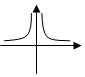
A． B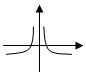． C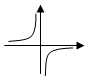． D．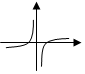
組卷：14引用：5難度：0.9
解析
4．已知條件p：x＞1，條件
q
：
1
x
≤
1
，則p是q的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既非充分也非必要條件
組卷：50引用：13難度：0.9
解析
5．冪函數f（x）=x^α的圖象過點（2，4），那么函數f（x）的單調遞增區間是（　　）
A．（-2，+∞） B．[-1，+∞） C．[0，+∞） D．（-∞，-2）
組卷：1014引用：15難度：0.7
解析
6．若函數y=f（x）為偶函數，則函數y=f（x+1）的一條對稱軸是（　　）
A．x=2 B．x=1 C．x=0 D．x=-1
組卷：28引用：4難度：0.5
解析
7．已知集合A={x|x²-2x+a＞0}，且1?A，則實數a的取值范圍是（　　）
A．（-∞，1） B．（-∞，1] C．[1，+∞） D．[0，+∞）
組卷：135引用：10難度：0.9
解析

21．某玩具廠計劃每天生產A、B、C三種玩具共100個．已知生產一個玩具A需5分鐘，生產一個玩具B需7分鐘，生產一個玩具C需4分鐘，而且總生產時間不超過10個小時．若每生產一個玩具A、B、C可獲得的利潤分別為5元、6元、3元．
（I）用每天生產的玩具A的個數x與玩具B的個數y表示每天的利潤T元；
（II）請你為玩具廠制定合理的生產任務分配計劃，使每天的利潤最大，并求最大利潤．
組卷：27引用：3難度：0.3
解析
22．某光學儀器廠有一條價值為a萬元的激光器生產線，計劃通過技術改造來提高該生產線的生產能力，提高產品的增加值．經過市場調查，產品的增加值y萬元與技術改造投入x萬元之間滿足：
①y與（a-2x）?x²成正比；
②當
x
=
a
4
時，
y
=
a
3
8
，并且技術改造投入滿足
x
a
-
x
∈
（
0
，
t
]
，其中t為常數且t∈（1，2]．
（I）求y=f（x）表達式及定義域；
（Ⅱ）求技術改造之后，產品增加值的最大值及相應x的值．
組卷：18引用：3難度：0.5
解析