2022-2023學年江蘇省常州市聯盟學校高一(下)學情調研數學試卷(3月份)
發布:2024/7/19 8:0:9
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知向量
=(4,2),a=(x,3),且b∥a,則x等于( )bA.9 B.6 C.5 D.3 組卷:488引用:16難度:0.9 -
2.sin160°cos10°+cos20°sin10°=( )
A. -32B. 32C. 12D. -12組卷:202引用:18難度:0.9 -
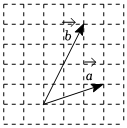 3.已知向量,a在正方形網格中的位置如圖所示,那么向量b與a-b的夾角為( )b
3.已知向量,a在正方形網格中的位置如圖所示,那么向量b與a-b的夾角為( )bA.45° B.60° C.90° D.135° 組卷:60引用:3難度:0.8 -
4.密位制是度量角的一種方法,把一周角等分為6000份,每一份叫做1密位的角.在角的密位制中,單位可省去不寫,采用四個數碼表示角的大小,在百位數與十位數之間畫一條短線,如7密位寫成“0-07”,478密位寫成“4-78”.如果一個半徑為4的扇形,其圓心角用密位制表示為6-25,則該扇形的面積為( )
A. 10π3B.2π C. 5π3D. 5π6組卷:34引用:2難度:0.8 -
5.已知A(-3,0),B(0,2),O為坐標原點,點C在∠AOB內,|
|=2OC,且∠AOC=2,設π4=OC+λOA(λ∈R),則λ的值為( )OBA.1 B. 13C. 12D. 23組卷:118引用:8難度:0.7 -
6.在平面直角坐標系xOy中,α為第四象限角,角α的終邊與單位圓O交于點P(x0,y0),若
,則y0=( )cos(α-π3)=-33A. -3-326B. 3-326C. -6-36D. -6+36組卷:35引用:3難度:0.7 -
7.已知A是函數
的最大值,若存在實數x1,x2使得對任意實數x總有f(x1)≤f(x)≤f(x2)成立,則A|x1-x2|的最小值為( )f(x)=3sin(2023x+π4)+sin(2023x-π4)A. π2023B. 2π2023C. 3π2023D. 4π2023組卷:94引用:3難度:0.7
四、解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
21.已知梯形ABCD中,
,AB=BC=2,∠ABC=60°,E為BC的中點,連接AE.AB=2DC
(1)若,求證:B,F,D三點共線;AF=4FE
(2)求與AE所成角的余弦值;BD
(3)若P為以B為圓心、BA為半徑的圓弧(包含A,C)上的任意一點,當點P在圓弧?AC(包含A,C)上運動時,求?AC的最小值.PA?PC組卷:98引用:3難度:0.6 -
22.已知向量
,a=(cosx,cos2x).設函數b=(sin(x+π6),-1),x∈R.f(x)=2a?b+12
(1)求函數f(x)的解析式及其單調增區間;
(2)設,若方程2g(x)-m=1在g(x)=f(x+π4)上有兩個不同的解x1,x2,求實數m的取值范圍,并求tan(x1+x2)的值.x∈[0,π2]
(3)若將y=f(x)的圖像上的所有點向左平移個單位,再把所得圖像上所有點的橫坐標伸長為原來的2倍(縱坐標不變),得到函數h(x)的圖像.當π4(其中m∈[0,π])時,記函數h(x)的最大值與最小值分別為h(x)max與h(x)min,設φ(m)=h(x)max-h(x)min,求函數φ(m)的解析式.x∈[m,m+π2]組卷:87引用:4難度:0.6


