2022-2023學年四川省成都市石室中學教育集團九年級（上）期中數學試卷

一、選擇題（每小題4分，共32分）

• 1．如圖所示的幾何體的左視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：47引用：1難度：0.8

  解析

• 2．根據表格中的數據，估計一元二次方程ax²+bx+c=6（a,b,c為常數，a≠0）一個解x的范圍為（　　）
  

  x	0.5	1	1.5	2	3
  ax2+bx+c	28	18	10	4	-2

  A．0.5＜x＜1

  B．1＜x＜1.5

  C．1.5＜x＜2

  D．2＜x＜3
  組卷：534引用：5難度：0.6

  解析

• 3．如圖，已知△ABC∽△DEF，若∠A=30°，∠B=65°，則∠F的度數是（　　）

  A．30°

  B．85°

  C．35°

  D．100°
  組卷：103引用：4難度：0.7

  解析

• 4．如圖，已知△A′B′C′與△ABC是位似圖形，點O是位似中心，若A′是OA的中點，則△A′B'C′與△ABC的面積比是（　　）

  A．1：4

  B．1：2

  C．2：1

  D．4：1
  組卷：1323引用：5難度：0.6

  解析

• 5．某數學活動小組在利用太陽光線測量某棵樹AB的高度時，發現樹AB的影子不全落在地面上，有一部分影子落在教學樓的墻壁上．經測量，落在墻壁上影高CD為2米，落在地面上的影長BC為5米，同一時間測得8米高的國旗桿影長是4米，則樹高為（　　）

  A．8米

  B．10米

  C．12米

  D．14米
  組卷：202引用：3難度：0.7

  解析

• 6．下列命題中，是真命題的是（　　）

  A．一條線段上只有一個黃金分割點

  B．各角分別相等，各邊成比例的兩個多邊形相似

  C．兩條直線被一組平行線所截，所得的線段成比例

  D．若2x=3y,則 x y = 2 3
  組卷：1434引用：6難度：0.7

  解析

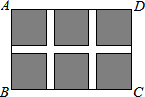• 7．如圖，某小區規劃在一個長30m、寬20m的長方形土地ABCD上修建三條同樣寬的通道，使其中兩條與AB平行，另一條與AD平行，其余部分鐘花草，要使每一塊花草的面積都為78cm²，那么通道寬應設計成多少m？設通道寬為xm,則由題意列得方程為（　　）

  A．（30-x）（20-x）=78	B．（30-2x）（20-2x）=78
  C．（30-2x）（20-x）=6×78	D．（30-2x）（20-2x）=6×78
  組卷：879引用：19難度：0.9

  解析

• 8．如圖，矩形ABCD中，點E，點F分別是BC，CD的中點，AE交對角線BD于點G，BF交AE于點H．則

  GH

  HE

  的值是（　　）

  A． 1 2

  B． 2 3

  C． 2 2

  D． 3 2
  組卷：3557引用：10難度：0.5

  解析

二、填空題（本大題共5小題，每小題4分，共20分）

• 9．已知：

  a

  b

  =

  1

  2

  ，則

  a

  +

  b

  b

  =

  ．
  組卷：1362引用：43難度：0.9

  解析

二、解答題（共30分）

• 26．【證明體驗】
  （1）如圖1，AD為△ABC的角平分線，∠ADC=60°，點E在AB上，AE=AC．求證：DE平分∠ADB．
  【思考探究】
  （2）如圖2，在（1）的條件下，F為AB上一點，連結FC交AD于點G．若FB=FC，DG=2，CD=3，求BD的長．
  【拓展延伸】
  （3）如圖3，在四邊形ABCD中，對角線AC平分∠BAD，∠BCA=2∠DCA，點E在AC上，∠EDC=∠ABC．若BC=5，CD=2

  5

  ，AD=2AE，求AC的長．
  
  組卷：5874引用：24難度：0.3

  解析

• 27．如圖，在平面直角坐標系中，直線AB與x軸交于點B，與y軸交于點A，OA=1，

  OB

  =

  3

  OA

  ，直線

  OC

  ：

  y

  =

  3

  x

  交直線AB于點C．
  
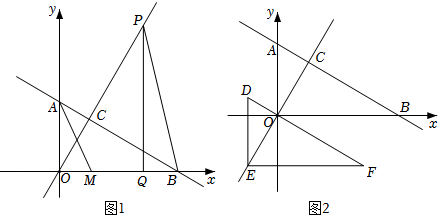
  （1）求直線AB的解析式及C點的坐標；
  （2）如圖1，P為直線OC上一動點且在第一象限內，M、Q為x軸上動點，Q在M右側且

  MQ

  =

  3

  2

  ，當

  S

  △

  PCB

  =

  9

  3

  8

  時，求PQ+QM+MA最小值；
  （3）如圖2，將△AOB沿著射線CO方向平移，平移后A、O、B三點分別對應D、E、F三點，當DF過O點時，在平面內是否存在H點，在第一象限內是否存在N點，使得以H、N、D、F四個點為頂點的四邊形為正方形，若存在，請直接寫出H點坐標；若不存在，請說明理由．
  組卷：1383引用：6難度：0.3

  解析