2022-2023學年四川省涼山州安寧河聯盟高一(下)期中數學試卷
發布:2024/7/8 8:0:10
一、單選題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知平面向量
,a=(m+1,-2).若b=(-3,2),則實數m的值為( )a∥bA.-4 B. -73C.2 D.4 組卷:43引用:2難度:0.8 -
2.要得到函數y=sin(2x-
)的圖象,只需要將函數y=sin2x的圖象( )π3A.向左平移 個單位π3B.向左平移 個單位π6C.向右平移 個單位π3D.向右平移 個單位π6組卷:932引用:34難度:0.9 -
3.cos37°sin67°-sin37°cos67°的值為( )
A. -32B. -12C. 12D. 32組卷:44引用:2難度:0.7 -
4.若函數f(x)=2sin(2x+φ)的圖像關于y軸對稱,則φ的值可能為( )
A. π3B.π C. -π2D. π6組卷:212引用:3難度:0.7 -
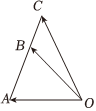 5.如圖,若,OA=a,OB=b,點B是線段AC上一點,且OC=c.若AB=32BC,則( )b=λa+μc
5.如圖,若,OA=a,OB=b,點B是線段AC上一點,且OC=c.若AB=32BC,則( )b=λa+μcA. ,λ=15μ=45B. ,λ=25μ=35C. ,λ=35μ=25D. ,λ=45μ=15組卷:98引用:2難度:0.5 -
6.已知
,則sin(α+π6)=14=( )cos(2α+π3)A. 78B. -78C. 1516D. -1516組卷:118引用:3難度:0.8 -
7.函數
的單調遞增區間為( )y=13tan(2x-π6)+12A. (kπ-π6,kπ+π3)(k∈Z)B. (kπ+π6,kπ+5π12)(k∈Z)C. (kπ2-π6,kπ2+π3)(k∈Z)D. (kπ2+π6,kπ2+5π12)(k∈Z)組卷:259引用:3難度:0.9
四、解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
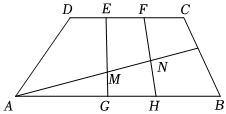 21.如圖,在梯形ABCD中,,E、F是DC的兩個三等分點,G,H是AB的兩個三等分點,線段BC上一動點P滿足AB=2DC.AP分別交EG、FH于M,N兩點,記BP=λBC(0≤λ≤1),AB=a.AD=b
21.如圖,在梯形ABCD中,,E、F是DC的兩個三等分點,G,H是AB的兩個三等分點,線段BC上一動點P滿足AB=2DC.AP分別交EG、FH于M,N兩點,記BP=λBC(0≤λ≤1),AB=a.AD=b
(1)當時,用λ=13,a表示b;AP
(2)若,求μ的最大值.MN=μAP組卷:80引用:3難度:0.5 -
22.已知函數
,函數f(x)的圖象經過點f(x)=3cos(2ωx+φ)+1(ω>0,|φ|<π2)且f(x)的最小正周期為(-π12,1).π2
(1)求函數f(x)的解析式;
(2)若對任意x∈[0,2π]恒成立,求實數m的取值范圍;2m[1+3(f(x8-π12)-1)]+cosx+1≤0
(3)將函數y=f(x)圖象上所有的點向下平移1個單位長度;再將函數圖象上所有點的橫坐標變為原來的2倍,縱坐標不變;再將圖象上所有的點的橫坐標不變,縱坐標變為原來的倍,得到函數y=h(x)圖象,令函數g(x)=h(x)+1,區間[a,b](a,b∈R且a<b)滿足:y=g(x)在[a,b]上至少有18個零點,在所有滿足上述條件的[a,b]中,求b-a的最小值.233組卷:197引用:2難度:0.3


