當前位置：試卷中心 > 試卷詳情

2023-2024學年重慶八中高一（上）期中數學試卷

發布：2024/10/3 14:0:2

一、單選題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．若P={（1，2），（1，3）}，則集合P中元素的個數是（　　）
A．1 B．2 C．3 D．4
組卷：34引用：4難度：0.9
解析
2．命題“?x∈R，x²-2x+12≤0”的否定為（　　）
A．?x₀∈R，x₀²-2x₀+12＞0 B．?x∈R，x²-2x+12≥0
C．?x?R，x²-2x+12≤0 D．?x₀?R，x₀²-2x₀+12＞0
組卷：221引用：8難度：0.8
解析
3．已知集合
A
=
{
α
|
α
=
π
3
+
kπ
，
k
∈
Z
}
，
B
=
{
β
|
β
=
2
π
3
+
kπ
3
，
k
∈
Z
}
，下列描述正確的是（　　）
A．A∩B=A B．A∩B=B
C．A∩B=? D．以上選項都不對
組卷：29引用：1難度：0.7
解析
4．若x＞3，則
x
2
-
6
x
+
11
x
-
3
的最小值為（　　）
A．2 B．
2
C．
4
2
D．
2
2
組卷：301引用：3難度：0.9
解析
5．已知p：m²-8m＜0，q：關于x的不等式x²+（m-4）x+9＞0的解集為R，則p是q的（　　）
A．充分不必要條件 B．必要不充分條件
C．既不充分也不必要條件 D．充要條件
組卷：78引用：1難度：0.8
解析
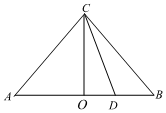6．數學里有一種證明方法叫做Proofswithoutwords,也稱之為無字證明，一般是指僅用圖象語言而無需文字解釋就能不證自明的數學命題，由于這種證明方法的特殊性，無字證明被認為比嚴格的數學證明更為優雅．現有如圖所示圖形，在等腰直角三角形ABC中，點O為斜邊AB的中點，點D為斜邊AB上異于頂點的一個動點，設AD=a,BD=b,則該圖形可以完成的無字證明為（　　）
A．
a
+
b
2
≥
ab
（
a
＞
0
，
b
＞
0
）
B．
a
+
b
2
≤
a
2
+
b
2
2
（
a
＞
0
，
b
＞
0
）
C．
2
ab
a
+
b
≤
ab
（
a
＞
0
，
b
＞
0
）
D．
a
2
+
b
2
≥
2
ab
（
a
＞
0
，
b
＞
0
）
組卷：559引用：8難度：0.5
解析
7．已知a＞0，b＞0且ab=1，不等式
1
2
a
+
1
2
b
+
m
a
+
b
≥4恒成立，則正實數m的取值范圍是（　　）
A．m≥2 B．m≥4 C．m≥6 D．m≥8
組卷：588引用：17難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共70分．請將正確答案做在答題卷相應位置，要有必要的推理或證明過程．）

21．已知函數f（x）為R上的奇函數，當x＜0時，
f
（
x
）
=
-
x
+
a
x
-
2
．
（1）求f（x）的解析式；
（2）若函數f（x）在[2，+∞）上單調遞減，求實數a的取值范圍．
組卷：75引用：3難度：0.5
解析
22．若在函數f（x）的定義域內存在區間[a,b]，使得f（x）在[a,b]上單調，且函數值的取值范圍是[ma,mb]（m是常數），則稱函數f（x）具有性質M．
（1）當
m
=
1
2
時，函數
f
（
x
）
=
x
否具有性質M？若具有，求出a,b；若不具有，說明理由；
（2）若定義在（0，2）上的函數
f
（
x
）
=
|
x
+
4
x
-
5
|
具有性質M，求m的取值范圍．
組卷：126引用：4難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．?x₀∈R，x₀²-2x₀+12＞0	B．?x∈R，x²-2x+12≥0
C．?x?R，x²-2x+12≤0	D．?x₀?R，x₀²-2x₀+12＞0

A．充分不必要條件	B．必要不充分條件
C．既不充分也不必要條件	D．充要條件

A． a + b 2 ≥ ab （ a ＞ 0 ， b ＞ 0 ）	B． a + b 2 ≤ a 2 + b 2 2 （ a ＞ 0 ， b ＞ 0 ）
C． 2 ab a + b ≤ ab （ a ＞ 0 ， b ＞ 0 ）	D． a 2 + b 2 ≥ 2 ab （ a ＞ 0 ， b ＞ 0 ）

A．A∩B=A	B．A∩B=B
C．A∩B=?	D．以上選項都不對

2023-2024學年重慶八中高一（上）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．若P={（1，2），（1，3）}，則集合P中元素的個數是（ ）

2．命題“?x∈R，x2-2x+12≤0”的否定為（ ）

3．已知集合A={α|α=π3+kπ，k∈Z}，B={β|β=2π3+kπ3，k∈Z}，下列描述正確的是（ ）

4．若x＞3，則x2-6x+11x-3的最小值為（ ）

5．已知p：m2-8m＜0，q：關于x的不等式x2+（m-4）x+9＞0的解集為R，則p是q的（ ）

7．已知a＞0，b＞0且ab=1，不等式12a+12b+ma+b≥4恒成立，則正實數m的取值范圍是（ ）

四、解答題（本大題共6小題，共70分．請將正確答案做在答題卷相應位置，要有必要的推理或證明過程．）

21．已知函數f（x）為R上的奇函數，當x＜0時，f（x）=-x+ax-2．（1）求f（x）的解析式；（2）若函數f（x）在[2，+∞）上單調遞減，求實數a的取值范圍．

1．若P={（1，2），（1，3）}，則集合P中元素的個數是（　　）

2．命題“?x∈R，x²-2x+12≤0”的否定為（　　）

3．已知集合
A
=
{
α
|
α
=
π
3
+
kπ
，
k
∈
Z
}
，
B
=
{
β
|
β
=
2
π
3
+
kπ
3
，
k
∈
Z
}
，下列描述正確的是（　　）

4．若x＞3，則
x
2
-
6
x
+
11
x
-
3
的最小值為（　　）

5．已知p：m²-8m＜0，q：關于x的不等式x²+（m-4）x+9＞0的解集為R，則p是q的（　　）

7．已知a＞0，b＞0且ab=1，不等式
1
2
a
+
1
2
b
+
m
a
+
b
≥4恒成立，則正實數m的取值范圍是（　　）

21．已知函數f（x）為R上的奇函數，當x＜0時，
f
（
x
）
=
-
x
+
a
x
-
2
．
（1）求f（x）的解析式；
（2）若函數f（x）在[2，+∞）上單調遞減，求實數a的取值范圍．