2023年福建省泉州市南安實驗中學中考數學考前適應試卷(6月份)
發布:2024/5/31 8:0:9
一、選擇題:本題共10小題,每小題4分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求.在答題卡的相應位置內作答.
-
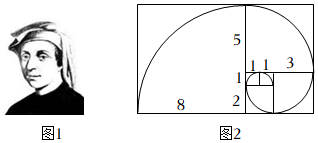 1.“生活中并不缺少美,而是缺乏發現美的眼睛”——羅丹,美在數學中也不曾少有.如圖,是以斐波那契數列的每一項的數為邊長畫6個小正方形組成的一個大長方形.每個小正方形畫出四分之一圓弧,使相鄰的圓弧首尾相連,這些圓弧組成的平滑曲線稱為斐波那契螺旋線.試求圖中斐波那契螺旋線的長( )(π取3.14)
1.“生活中并不缺少美,而是缺乏發現美的眼睛”——羅丹,美在數學中也不曾少有.如圖,是以斐波那契數列的每一項的數為邊長畫6個小正方形組成的一個大長方形.每個小正方形畫出四分之一圓弧,使相鄰的圓弧首尾相連,這些圓弧組成的平滑曲線稱為斐波那契螺旋線.試求圖中斐波那契螺旋線的長( )(π取3.14)A.15.7 B.31.4 C.9.8596 D.37.68 組卷:201引用:6難度:0.6 -
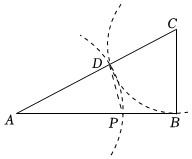 2.如圖,已知BC⊥AB,BC=AB,試求12的小數部分( )APAB
2.如圖,已知BC⊥AB,BC=AB,試求12的小數部分( )APABA.0.118 B. 5-0.5C. 1.5-0.55D.0.618 組卷:57引用:1難度:0.5 -
3.若實數a,b,c滿足條件
,則a,b,c中( )1a+1b+1c=1a+b+cA.必有兩個數相等 B.必有兩個數互為相反數 C.必有兩個數互為倒數 D.每兩個數都不等 組卷:4872引用:10難度:0.7 -
4.y=
最大值與最小值之和為( )x2-x+1x2+x+1A.1 B.10 C. 103D. 132組卷:279引用:3難度:0.6 -
5.某大學畢業生為自主創業于2021年8月初向銀行貸款360000元,與銀行約定按“等額本金還款法”分10年進行還款,從2021年9月初開始,每個月月初還一次款,貸款月利率為0.5%,現因經營狀況良好,準備向銀行申請提前還款,計劃于2026年8月初將剩余貸款全部一次還清,則該大學畢業生按現計劃的所有還款數額比按原約定所有還款數額少( )(注:“等額本金還款法”是將本金平均分配到每一期進行償還,每一期所還款金額由兩部分組成.一部分為每期本金,即貸款本金除以還款期數;另一部分是利息,即貸款本金與已還本金總額的差乘以利率.1年按12個月計算)
A.18300元 B.22450元 C.27450元 D.28300元 組卷:112引用:3難度:0.3 -
6.在拋物線y=a(x-m-1)2+c(a≠0)和直線y=-
x的圖象上有三點(x1,m)、(x2,m)、(x3,m),則x1+x2+x3的結果是( )12A. -32m+12B.0 C.1 D.2 組卷:1713引用:7難度:0.5 -
7.若方程x2-2x-t=0在-1<x≤4范圍內有實數根,則t的取值范圍為( )
A.3<t≤8 B.-1≤t≤3 C.-1<t≤8 D.-1≤t≤8 組卷:2408引用:7難度:0.7 -
8.已知C為線段AB外一點.假設尺規作圖作四邊形ABCD,使得CD∥AB,且CD=2AB,四邊形ABCD中,AC,BD相交于點P,AB,CD的中點分別為M,N,則M,P,N三點間關系為( )
A.共圓 B.共線 C.重合 D.相離 組卷:80引用:3難度:0.3
三、解答題:本題共9小題,共86分.解答應寫出文字說明,證明過程或演算步驟.在答題卡的相應位置內作答.
-
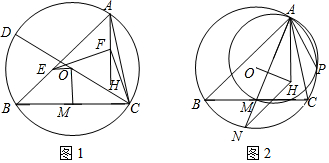 24.如圖1,設△ABC是一個銳角三角形,且AB≠AC,Γ為其外接圓,O、H分別為其外心和垂心,CD為圓Γ直徑,M為線段BC上一動點且滿足AH=2OM.
24.如圖1,設△ABC是一個銳角三角形,且AB≠AC,Γ為其外接圓,O、H分別為其外心和垂心,CD為圓Γ直徑,M為線段BC上一動點且滿足AH=2OM.
(1)證明:M為BC中點;
(2)過O作BC的平行線交AB于點E,若F為AH的中點,證明:EF⊥FC;
(3)直線AM與圓Γ的另一交點為N(如圖2),以AM為直徑的圓與圓Γ的另一交點為P.證明:若AP、BC、OH三線共點,則AH=HN;反之也成立.組卷:192引用:3難度:0.3 -
25.如圖,已知拋物線y=
(x+2)(x-4)(k為常數,且k>0)與x軸從左至右依次交于A,B兩點,與y軸交于點C,經過點B的直線y=-k8x+b與拋物線的另一交點為D.33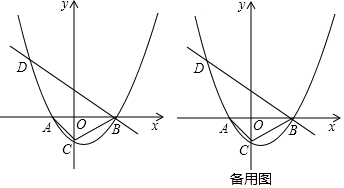
(1)若點D的橫坐標為-5,求拋物線的函數表達式;
(2)在(1)條件下,設F為線段BD上一點(不含端點),連接AF,一動點M從點A出發,沿線段AF以每秒1個單位的速度運動到F,再沿線段FD以每秒2個單位的速度運動到D后停止.當點F的坐標是多少時,點M在整個運動過程中用時最少?組卷:1058引用:5難度:0.3


