2022年寧夏銀川十中中考數(shù)學二模試卷

一、選擇題。（本大題共8個小題，每小題3分，共24分。）

• 1．下列計算正確的是（　　）

  A． 2 + 5 = 7

  B．2a+3a=6a

  C．（ab2）2=ab4

  D．a(chǎn)?a3=a4
  組卷：45引用：4難度：0.7

  解析

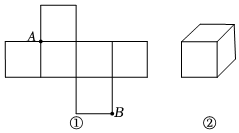• 2．圖①是邊長為1的六個小正方形組成的圖形，它可以圍成圖②的正方體，則圖①中正方形頂點A，B在圍成的正方體上的距離是（　　）

  A．2 2

  B． 2

  C． 5

  D．1
  組卷：31引用：2難度：0.8

  解析

• 3．不等式組

  2 x - 2 ≤ 0

  x ＞ - 1

  的解集在數(shù)軸上表示為（　　）

  A．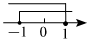

  B．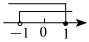

  C．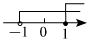

  D．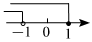
  組卷：102引用：2難度：0.8

  解析

• 4．下列說法正確的是（　　）

  A．一個游戲的中獎概率是 1 10  則做10次這樣的游戲一定會中獎

  B．為了解全國中學生的心理健康情況，應(yīng)該采用普查的方式

  C．一組數(shù)據(jù) 8，8，7，10，6，8，9 的眾數(shù)和中位數(shù)都是8

  D．若甲組數(shù)據(jù)的方差S2=0.01，乙組數(shù)據(jù)的方差S2=0.1，則乙組數(shù)據(jù)比甲組數(shù)據(jù)穩(wěn)定
  組卷：439引用：19難度：0.9

  解析

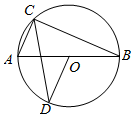• 5．如圖，AB是⊙O的直徑，點C在⊙O上，連接AC、BC，過點O作OD∥AC交⊙O于點D，點C、D在AB的異側(cè)，若∠B=24°，則∠BCD的度數(shù)是（　　）

  A．66°

  B．67°

  C．57°

  D．48°
  組卷：51引用：7難度：0.9

  解析

• 6．某工程隊準備修建一條長1200m的道路，由于采用新的施工方式，實際每天修建道路的速度比原計劃快20%，結(jié)果提前2天完成任務(wù)．若設(shè)原計劃每天修建道路x m,則根據(jù)題意可列方程為（　　）

  A． 1200 （ 1 - 20 % ） x - 1200 x =2	B． 1200 （ 1 + 20 % ） x - 1200 x =2
  C． 1200 x - 1200 （ 1 - 20 % ） x =2	D． 1200 x - 1200 （ 1 + 20 % ） x =2
  組卷：2287引用：82難度：0.7

  解析

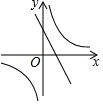• 7．一次函數(shù)y=ax+b與反比例函數(shù)y=

  c

  x

  的圖象如圖所示，則二次函數(shù)y=ax²+bx+c的大致圖象是（　　）

  A．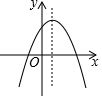

  B．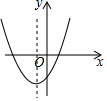

  C．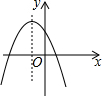

  D．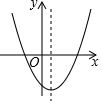
  組卷：1976引用：27難度：0.8

  解析

• 8．如圖，在菱形ABCD中，AB=4，∠C=60°，將菱形折疊，使點A恰好落在對角線BD上的G點處（不與B，D重合），折痕為EF，若DG=

  1

  3

  BG，則BE的長為（　　）

  A． 14 5

  B． 13 5

  C． 13 7

  D． 7 5
  組卷：475引用：4難度：0.4

  解析

四、解答題。（共36分）

• 25．為了防控新冠疫情，某地區(qū)積極推廣疫苗接種工作，衛(wèi)生防疫部門對該地區(qū)八周以來的相關(guān)數(shù)據(jù)進行收集整理，繪制得到圖表：
  該地區(qū)每周接種疫苗人數(shù)統(tǒng)計表
  

  周次	第1周	第2周	第3周	第4周	第5周	第6周	第7周	第8周
  接種人數(shù)（萬人）	7	10	12	18	25	29	37	42

  
  根據(jù)統(tǒng)計表中的數(shù)據(jù)，建立以周次為橫坐標，接種人數(shù)為縱坐標的平面直角坐標系，并根據(jù)以上統(tǒng)計表中的數(shù)據(jù)描出對應(yīng)的點，發(fā)現(xiàn)從第3周開始這些點大致分布在一條直線附近，現(xiàn)過其中兩點（3，12）、（8，42）作一條直線（如圖所示，該直線的函數(shù)表達式為y=6x-6），那么這條直線可近似反映該地區(qū)接種人數(shù)的變化趨勢．
  請根據(jù)以上信息，解答下列問題：
  （1）這八周中每周接種人數(shù)的平均數(shù)為

  萬人；該地區(qū)的總?cè)丝诩s為

  萬人；
  （2）若從第9周開始，每周的接種人數(shù)仍符合上述變化趨勢．
  ①估計第9周的接種人數(shù)約為

  萬人；
  ②專家表示：疫苗接種率至少達60%，才能實現(xiàn)全民免疫．那么，從推廣疫苗接種工作開始，最早到第幾周，該地區(qū)可達到實現(xiàn)全民免疫的標準？
  （3）實際上，受疫苗供應(yīng)等客觀因素，從第9周開始接種人數(shù)將會逐周減少a（a＞0）萬人，為了盡快提高接種率，一旦周接種人數(shù)低于20萬人時，衛(wèi)生防疫部門將會采取措施，使得之后每周的接種能力一直維持在20萬人．如果a=1.8，那么該地區(qū)的建議接種人群最早將于第幾周全部完成接種？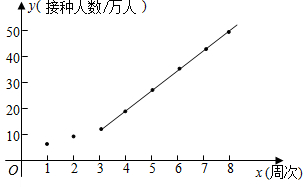
  組卷：921引用：3難度：0.5

  解析

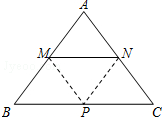• 26．在等腰△ABC中，AB=AC=5，BC=6．動點M、N分別在兩腰AB、AC上（M不與A、B重合，N不與A、C重合），且MN∥BC．將△AMN沿MN所在的直線折疊，使點A的對應(yīng)點為P．
  （1）當MN為何值時，點P恰好落在BC上？
  （2）當MN=x,△MNP與等腰△ABC重疊部分的面積為y,試寫出y與x的函數(shù)關(guān)系式．當x為何值時，y的值最大，最大值是多少？
  （3）是否存在x,使y等于S_△ABC的四分之一？如果存在，請直接寫出x的值；如果不存在，請說明理由．
  組卷：208引用：2難度：0.5

  解析